BINARY TO DECIMAL CONVERSION

The decimal number system that we used everyday contains ten digits, 0 through 9 and the base of this system is 10.

There is another very important number system known as Binary Number System which contains only two digits, 0 and 1. So the base of binary number system is 2.

To avoid confusion while using different numeral systems, the base of each individual number may be specified by writing it as subscript of the number.

For example, the decimal number 156 will be written as 15610. The binary number 10011100 will be specified as 100111002.

In the binary system, only 2 digits are used, namely 0 and 1. The positional values in a base 2 system are ….,

2⁴, 2³, 2², 2¹, 2⁰

Note : There is no 2 in base 2.

For (1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1111, …..)

For example, the number 10011 (base 2) means :

=  1 x 2⁴ + 0 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2⁰  

=  16 + 0 + 0 + 2 + 1  

=  19 (base 10)

Converting Binary to Decimal - Example

A binary number 11001 (base 2) can be converted into decimal number (base 10) using the method explained below. 

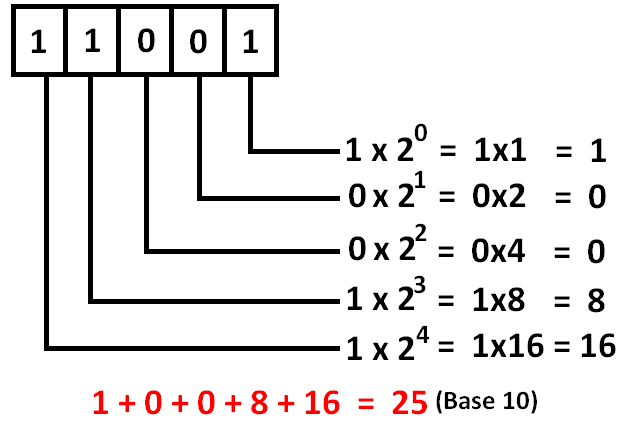
Therefore, the binary number 11001 (base 2) is equal to the decimal number 25 (base 10)

Do you want to check your answer fro the questions like "Decimal to binary" or "Binary to decimal" ?

Please click on the following links to get answer instantly for your questions. 

Binary to decimal online converter

Decimal to binary online converter

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.