BOX PLOTS

A box plot is a display that shows how the values in a data set are distributed, or spread out. To make a box-plot, first find five values for the data set :

• the least value
• the lower quartile — the median of the lower half of the data
• the median
• the upper quartile — the median of the upper half of the data
• the greatest value

The picture given below clearly illustrates a box-plot. 

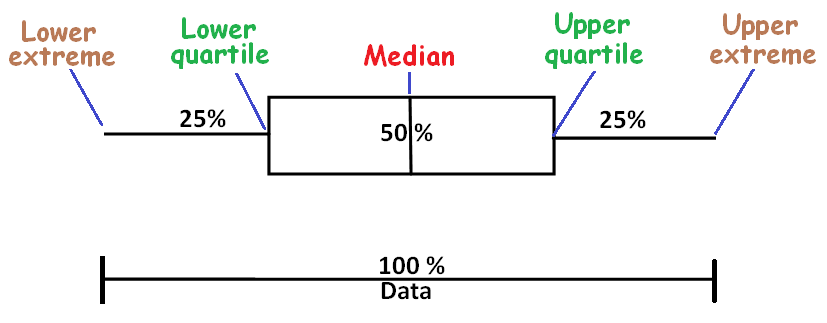
In the above figure, the box spans interquartile range (central 50%).

To draw box-plot graph for a data set, we have to know lower quartile, upper quartile and median.  

Example 1 :

Make a box-plot for the data given below. 

4.3,  5.1,  3.9,  4.5,  4.4,  4.9,  5.0,  4.7,  4.1,  4.6,  4.4,  4.3,  4.8,  4.4,  4.2,  4.5,  4.4

Solution :

Making box plot :

Step 1 :

Let us write the observations in the data in ascending order. 

3.9,  4.1,  4.2,  4.3,  4.3,  4.4,  4.4,  4.4,  4.4,  4.5,  4.5,  4.6,  4.7,  4.8,  4.9,  5.0,  5.1

Step 2 :

Number of observations (n) = 17.

Let us find lower quartile, upper quartile and median.

Lower Quartile :

To find the lower quartile, find the value of ⁽ⁿ ⁺ ¹⁾⁄₄.

= ⁽ⁿ ⁺ ¹⁾⁄₄

= ⁽¹⁷ ⁺ ¹⁾⁄₄

= ¹⁸⁄₄

= 4.5

Lower quartile comes in between 4^th and 5^th observations.

So, lower quartile is equal to average of 4^th and 5^th observations.

Lower quartile :

= ⁽⁴^.³ ⁺ ⁴^.³⁾⁄₂

= ⁸^.⁶⁄₂

= 4.3

Upper Quartile :

To find the upper quartile, find the value of ³⁽ⁿ ⁺ ¹⁾⁄₄.

= ³⁽ⁿ ⁺ ¹⁾⁄₄

= ³⁽¹⁷ ⁺ ¹⁾⁄₄

= ⁵⁴⁄₄

= 13.5

Upper quartile comes in between 13^th and 14^th observations.

So, upper quartile is equal to average of 13^th and 14^th observations.

Upper quartile :

= ⁽⁴^.⁷ ⁺ ⁴^.⁸⁾⁄₂

= ⁹^.⁵⁄₂

= 4.75

Median :

To find the upper quartile, find the value of ⁽ⁿ ⁺ ¹⁾⁄₂.

= ⁽ⁿ ⁺ ¹⁾⁄₂

= ⁽¹⁷ ⁺ ¹⁾⁄₂

= ¹⁸⁄₂

= 9

Median is exactly the 9^th observation. 

So, median = 4.4.

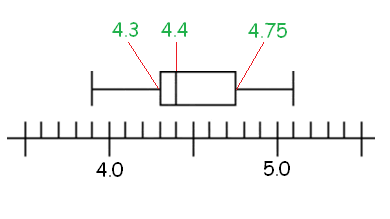
Step 3 :

Using lower quartile, upper quartile and median, we can make box-plot graph as given below.

Example 2 :

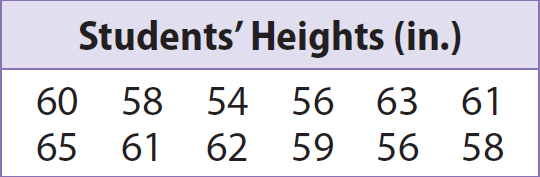
The heights of several students are shown. 

Make a box-plot for the data.

Solution :

Making box-plot :

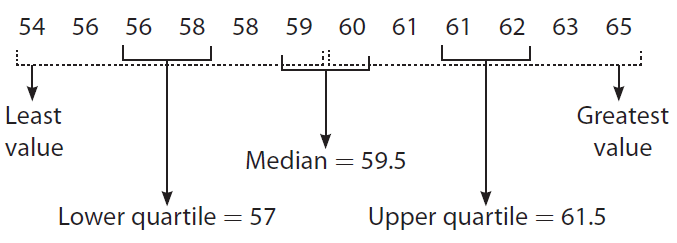
Step 1 :

Order the data and find the needed values.

Step 2 :

Draw the box-plot.

Draw a number line that includes all the data values.

On the number line, draw dots above the least value, the lower quartile, the median, the upper quartile, and the greatest value.

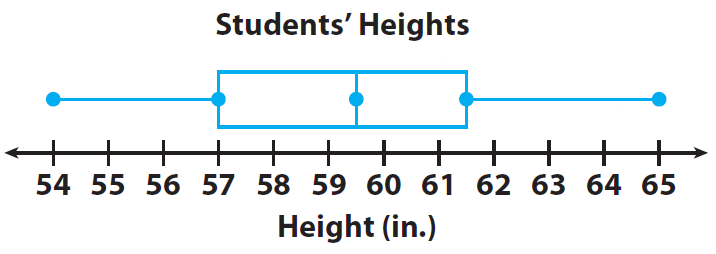
Reflect

In the example, what percent of the data values are included in the box portion ? What percent are included in each of the “whiskers” on the ends of the box ?

50%, 25%, 25%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.