CALCULATING COEFFICIENT OF VARIATION FROM MEAN AND STANDARD DEVIATION

Formula to calculate coefficient of variation from mean and standard deviation is  

=  (σ/x̄) ⋅ 100%

Here σ is the standard deviation and x̄ is the mean. 

Formula to find standard deviation σ is

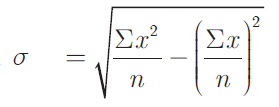
Formula to find arithmetic mean x̄ is

x̄  =  ∑x / n

Examples

Example 1 :

The standard deviation and mean of a data are 6.5 and 12.5 respectively. Find the coefficient of variation.

Solution :

Standard deviation  =  6.5

Mean  =  12.5

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

  =  (6.5/12.5) ⋅ 100%

  =  (65/125) ⋅ 100%

  =  (13/25) ⋅ 100%

  =  52%

So, the coefficient of variation is 52%.

Example 2 :

The standard deviation and coefficient of variation of a data are 1.2 and 25.6 respectively. Find the value of mean.

Solution :

Standard deviation  =  1.2

Coefficient of variation  =  25.6

mean  =  ?

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

25.6  =  (1.2/x̄) ⋅ 100%

x̄  =  (1.2/25.6) / 100%

  =  4.687

x̄  =  4.69

So, the required mean is 4.69

Example 3 :

If the mean and coefficient of variation of a data are 15 and 48 respectively, then find the value of standard deviation.

Solution :

Mean (x̄)  =  15

Coefficient of variation (C.V) =  48

Standard deviation (σ)  =  ?

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

48  =  (σ/15) ⋅ 100%

σ  =  (48 ⋅ 15) /100

  =  720/100

x̄  =  7.2

Example 4 :

If n = 5, x̄ = 6 , Σx² = 765 , then calculate the coefficient of variation.

Solution :

In order to find coefficient of variation, we must know standard deviation (σ)

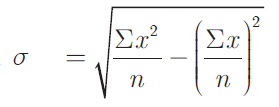
Σx²/n  =  765/5  =  153

(Σx/n)²  =  (x̄)²  =  6²  =  36

σ  =  √(153 - 36)

  =  √117

σ  =  3√13

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

C.V  =  (3√13)/6) ⋅ 100%

C.V  =  (3.60/2) ⋅ 100%

C.V  =  180.28%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.