CALCULATING SLOPE M

When the rate of change of a relationship is constant, any segment of its graph has the same steepness. The constant rate of change is called the slope of the line

The slope of a line is the ratio of the change in y-values (rise) for a segment of the graph to the corresponding change in x-values (run).

Let us consider the graph given below.  

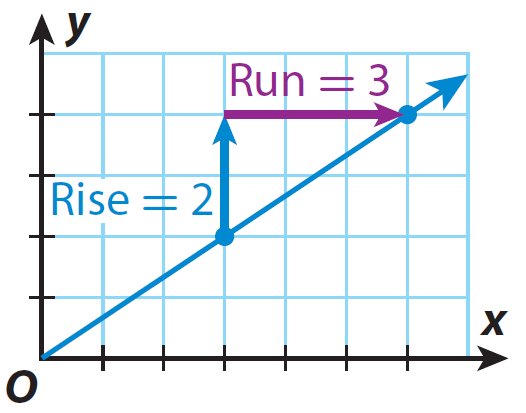
In the graph given above, for every 3 units of change on x-axis, there is a change of 2 units on y-axis.  

So, the slope of the line is 

=  Rise / Run

=  2/3

Slope formula

Let (x₁, y₁) and (x₂, y₂) be the two points on the a line. 

Then, the formula to find the slope of a straight line is

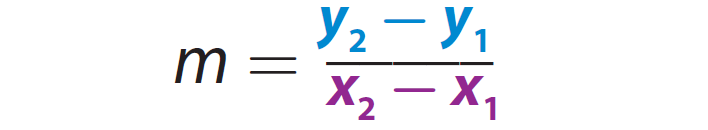
Solved Examples

Example 1 : 

Find m the slope of the line.

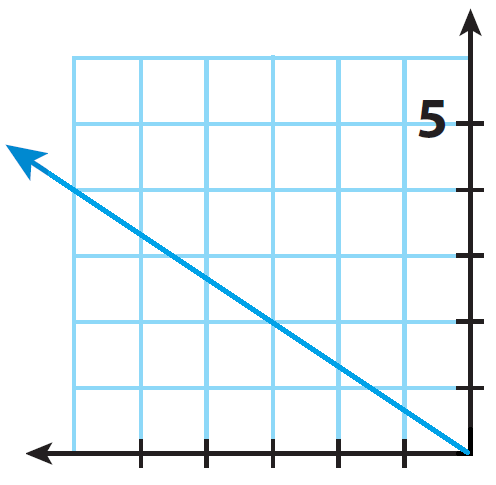
Solution :

Step 1 :

Choose two points on the line.

P₁(x₁, y₁) and P₂(x₂, y₂)

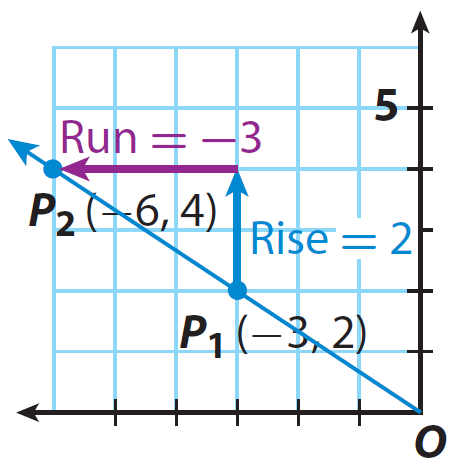
Step 2 :

Find the change in y-values (rise = y₂ - y₁) and the change in x-values (run = x₂ - x₁) as you move from one point to the other.

rise  =  y₂ - y₁     run  =  x₂ - x₁

rise  =  4 - 2     run  =  -6 - (-3)

rise  =  4 - 2     run  =  -6 +3

rise  =  2     run  =  -3

Step 3 :

m  =  rise / run

m  = (y₂ - y₁) / (x₂ - x₁)

m  =  2 / (-3)

m  =  -2/3

Example 2 : 

The graph shows the rate at which water is leaking from a tank. The slope of the line gives the leaking rate in gallons per minute. Find the slope of the line.

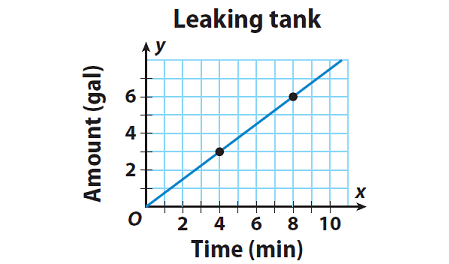
Solution :

Step 1 :

Choose two points on the line.

P(x₁, y₁)  =  P(4, 3)

Q(x₂, y₂)  =  Q(8, 6) 

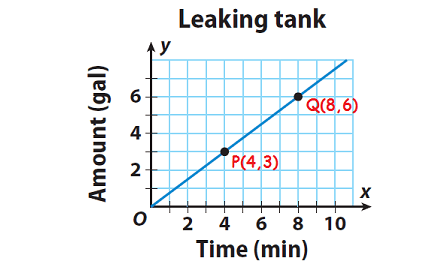
Step 2 :

Find the change in y-values (rise = y₂ - y₁) and the change in x-values (run = x₂ - x₁) as you move from one point to the other.

rise  =  y₂ - y₁     run  =  x₂ - x₁

rise  =  3 - 6     run  =  4 - 8

rise  =  -3     run  =  -4

Step 3 :

m  =  rise / run

m  = (y₂ - y₁) / (x₂ - x₁)

m  =  (-3) / (-4)

m  =  3/4

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.