CENTER OF DILATION OUTSIDE THE IMAGE

Example 1 :

The triangle PQR shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 3, graph the dilated image P'Q'R'.

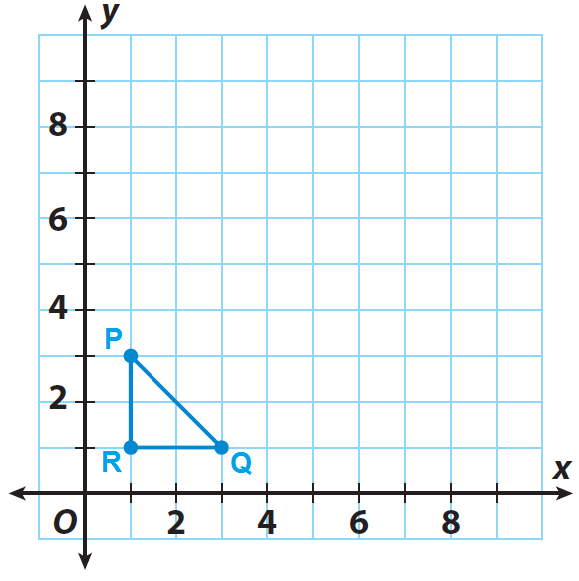
Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

P(1, 3), Q(3, 1) and R(1, 1)

Step 2 :

Since the scale factor is 3, the rule to get the coordinates of the vertices of the image is

 (x, y) → (3x, 3y)

Step 3 :

List the coordinates of the vertices of the image.

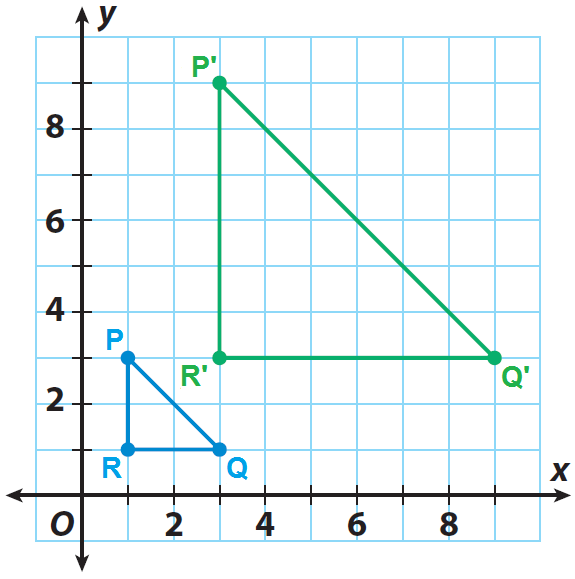
P(1, 3)  --->  P'(3, 9)

 Q(3, 1)  --->  Q'(9, 3)

R(1, 1)  --->  R'(3, 3)

Step 4 :

Graph the image P'Q'R'.

Example 2 :

The triangle ABC shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 1/3, graph the dilated image A'B'C'.

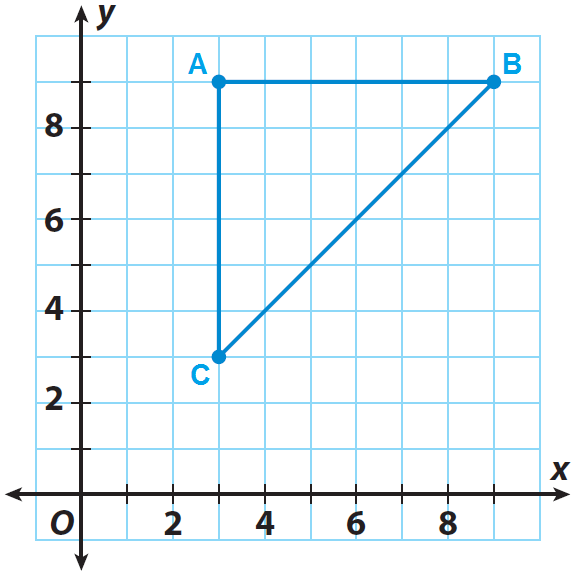
Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

A(3, 9), B(9, 9) and C(3, 3)

Step 2 :

Since the scale factor is 1/3, the rule to get the coordinates of the vertices of the image is

 (x, y) ---> [(1/3)x, (1/3)y]

Step 3 :

List the coordinates of the vertices of the image.

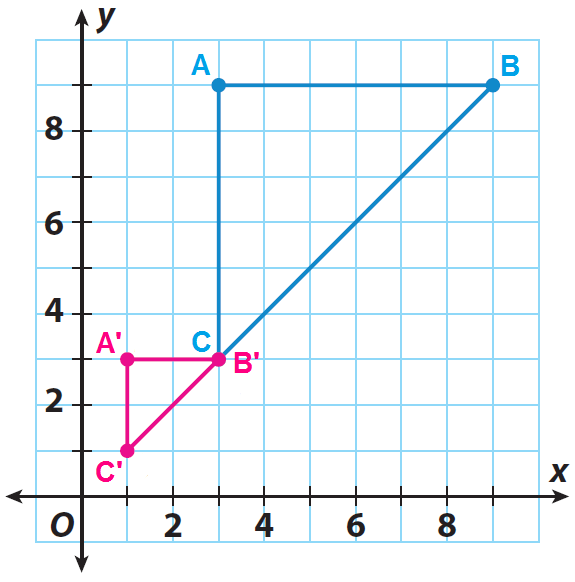
A(3, 9)  --->  A'(1, 3)

 B(9, 9)  --->  B'(3, 3)

C(3, 3)  --->  C'(1, 1)

Step 4 :

Graph the image A'B'C'.

Example 3 :

The rectangle JKLM shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 2, graph the dilated image J'K'L'M'.

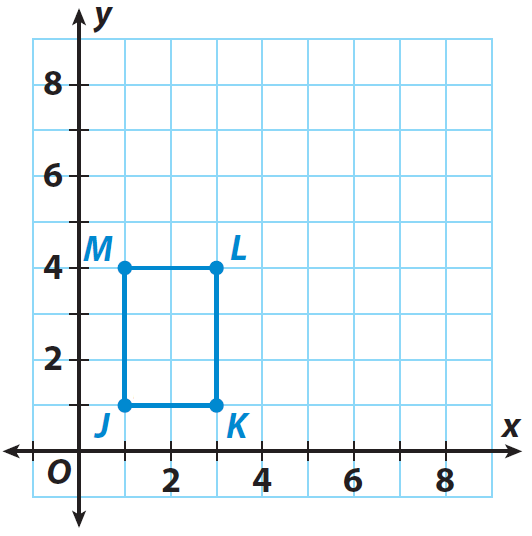
Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

J(1, 1), K(3, 1), L(3, 4) and M(1, 4)

Step 2 :

Since the scale factor is 2, the rule to get the coordinates of the vertices of the image is

 (x, y) ---> (2x, 2y)

Step 3 :

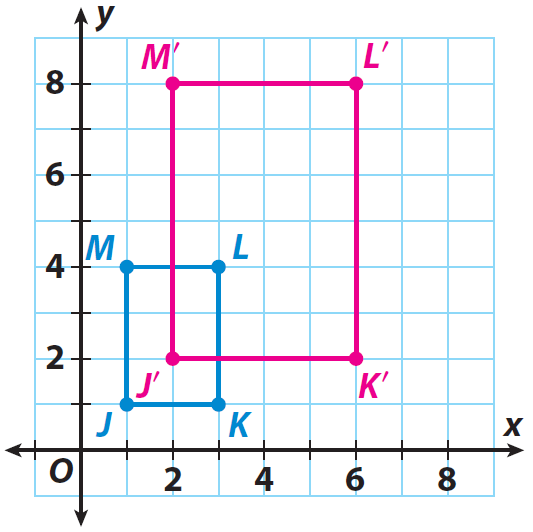
List the coordinates of the vertices of the image.

J(1, 1)  --->  J'(2, 2)

 K(3, 1)  --->  K'(6, 2)

L(3, 4)  --->  L'(6, 8)

M(1, 4)  --->  M'(2, 8)

Step 4 :

Graph the image J'K'L'M'.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.