CENTROID OF A TRIANGLE

The centroid of a triangle is the point of concurrency of the medians.

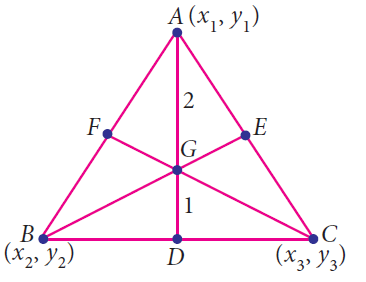
In the above triangle , AD, BE and CF are called medians. All the three medians AD, BE and CF are intersecting at G. So  G is called centroid of the triangle

If the coordinates of A, B and C are (x_1, y₁), (x_2, ,y₂) and (x₃, y₃), then the formula to determine the centroid of the triangle is given by

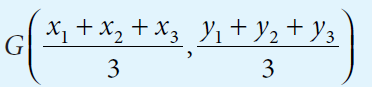
Examples

Example 1 :

Find the centroid of a triangle whose vertices are the points (8, 4), (1, 3) and (3, -1).

Solution :

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  8, x₂  =  1 and x₃  =  3

y₁  =  4, y₂  =  3 and y₃  =  -1

=  [(8 + 2 + 3)/3, (4 + 3 - 1)/3]

=  (12/3, 6/3)

=  (4, 2)

So, the centroid of the given triangle is (4, 2). 

Example 2 :

Find the centroid of a triangle whose vertices are the points (6, -1), (8, 3) and (10, -5).

Solution :

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  6, x₂  =  8 and x₃  =  10

y₁  =  -1, y₂  =  3 and y₃  =  -5

Then, 

=  [(6 + 8 + 10)/3, (-1 + 3 - 5)/3]

=  (24/3, -3/3)

=  (8, -1)

So, the centroid of the given triangle is (8, -1). 

Example 3 :

If a triangle has its centroid at (4, 3) and two of its vertices are (2, -1) and (7, 8), find the third vertex.

Solution :

Let (a, b) be the third vertex.

Centroid of the triangle  =  (4, 3)

[(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]  =  (4, 3)

x₁  =  2, x₂  =  7 and x₃  =  a

y₁  =  -1, y₂  =  8 and y₃  =  b

Then,

[(2 + 7 + a)/3, (-1 + 8 + b)/3]  =  (4, 3)

[(9 + a)/3, (7 + b)/3]  =  (4, 3)

Equate the coordinates of x and y. 

So, the third vertex is (3, 2).

Example 4 :

If the centroid of a triangle is (-2, 1) and two of its vertices are (1, -6) and (-5, 2), then find the third vertex.

Solution :

Let (a, b) be the third vertex.

Centroid of the triangle  =  (-2, 1)

[(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]  =  (-2, 1)

x₁  =  1, x₂  =  -5 and x₃  =  a

y₁  =  -6, y₂  =  2 and y₃  =  b

Then,

[(1 - 5 + a)/3, (-6 + 2 + b)/3]  =  (-2, 1)

[(-4 + a)/3, (-4 + b)/3]  =  (-2, 1)

Equate the coordinates of x and y. 

So, the third vertex is (-2, 7).

Example 5 :

Master gave a triangular plate with vertices (5, 8), (2, 4) and (8, 3) and a stick to a student. He wants to balance the plate on the stick. Can you help the boy to locate that point which can balance the plate ?

Solution :

The point which can balance the triangular plate is the centroid of the triangle. 

Formula to find centroid of a triangle is

= [(x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3]

x₁  =  5, x₂  =  2 and x₃  =  8

y₁  =  8, y₂  =  4 and y₃  =  3

=  [(5 + 2 + 8)/3, (8 + 4 + 3)/3]

=  (15/3, 15/3)

=  (5, 5)

So, the point which can balance the triangular plate is (5, 5). 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.