CHARACTERISTIC EQUATION OF MATRIX
Let A be any square matrix of order n x n and I be a unit matrix of same order. Then |A-λI| is called characteristic polynomial of matrix.
Then the equation |A-λI| = 0 is called characteristic roots of matrix. The roots of this equation is called characteristic roots of matrix.
Characteristic roots are also known as latent roots or eigenvalues of a matrix.
Example :
Determine the characteristic roots of the matrix
Solution :
|
Let A = |
|
|
Unit matrix of order 3x3, I = |
|
Multiply unit matrix I by λ.
= -λ(λ2 - 1) - 1[-λ - (-2)] + 2[-1 - (-2 λ)]
= -λ(λ2 - 1) - 1(-λ + 2) + 2 (-1 +2λ)
= -λ3 + λ + λ - 2 - 2 + 4λ
= -λ3 + 2λ - 2 - 2 + 4λ
= -λ3 + 6λ - 4
To find roots, equate |A-λI| to zero.
-λ3 + 6λ - 4 = 0
λ3 - 6λ + 4 = 0
By trial and error, we can check the values 1 or -1 or 2 or -2...... as a root for the above equation using synthetic division.
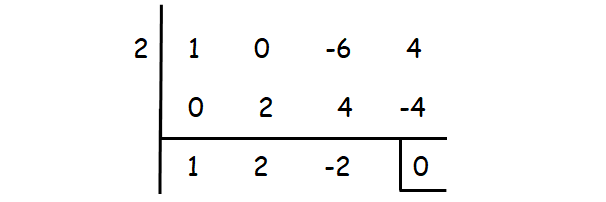
One of the roots is λ = 2.
To get the other two roots, solve the resulting equation λ2 + 2λ - 2 = 0 in the above synthetic division using quadratic formula.
λ = [-b ± √(b2 -4ac)]/2a
In λ2 + 2λ - 2 = 0, a = 1, b = 2 and c = -2.
Substitute the values of a, b and c in the quadratic formula.
λ = [-2 ± √(4 + 8)]/2
= [-2 ± √12]/2
= [-2 ± √12]/2
= [-2 ± 2√3]/2
= -1 ± √3
Therefore the characteristic roots are 1, -1 ± √3.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Markup and markdown word problems
Word problems on mixed fractions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and Venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Sum of all three four digit numbers formed using 0, 1, 2, 3
Sum of all three four digit numbers formed using 1, 2, 5, 6
©All rights reserved. onlinemath4all.com
Recent Articles
-
Exponential vs Linear Growth Worksheet
May 23, 22 01:59 AM
Exponential vs Linear Growth Worksheet
-
Linear vs Exponential Growth
May 23, 22 01:59 AM
Linear vs Exponential Growth - Concept - Examples
-
SAT Math Questions on Exponential vs Linear Growth
May 23, 22 01:34 AM
SAT Math Questions on Exponential vs Linear Growth