CHECKING IF THIS RELATION IS REFLEXIVE SYMMETRIC AND TRANSITIVE

Reflexive, Symmetric and transitive Relation

Let S be any non-empty set. Let R be a relation on S. Then

R is said to be reflexive if a is related to a for all a ∈ S.
R is said to be symmetric if a is related to b implies that b is related to a.
R is said to be transitive if “a is related to b and b is related to c” implies that a is related to c.

Question 1 :

Discuss the following relations for reflexivity, symmetricity and transitivity:

Let P denote the set of all straight lines in a plane. The relation R defined by “lRm if l is perpendicular to m”.

Solution :

Condition for reflexive :

R is said to be reflexive, if a is related to a for a ∈ S.

A line will not be perpendicular to itself. Hence it is not reflexive.

Condition for symmetric :

R is said to be symmetric, if a is related to b implies that b is related to a.

lRm that is, l perpendicular to m.

mRl, m is perpendicular to l, both are true. Hence it is symmetric.

Condition for transitive :

R is said to be transitive if “a is related to b and b is related to c” implies that a is related to c.

Let l, m and n be the set of lines in P.

If “l is related to m and m is related to n” implies that l is not related to n, because they l and n are parallel lines.

So, is transitive is not true.

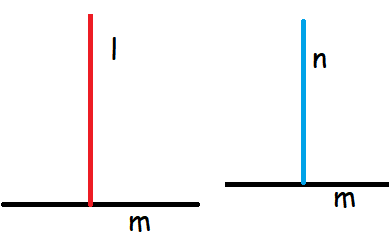
Hence P is relation which is reflexive but not symmetric and not transitive.

(iii) Let A be the set consisting of all the members of a family. The relation R defined by “aRb if a is not a sister of b”.

Solution :

Let A be the relation consisting of 4 elements mother (a), father (b), a son (c) and a daughter (d).

Condition for reflexive :

R is said to be reflexive, if a is related to a for a ∈ S.

Let "a" be a member of a relation A, a will be not a sister of a. Hence it is not reflexive.

Condition for symmetric :

R is said to be symmetric, if a is related to b implies that b is related to a.

aRb that is, a is not a sister of b.

bRc that is, b is not a sister of c.

dRc that is, d is a sister of c.

Hence it is not symmetric.

Condition for transitive :

R is said to be transitive if “a is related to b and b is related to c” implies that a is related to c.

dRa that is, d is not a sister of a.

aRc that is, a is not a sister of c. But a is a sister of c, this is not in the relation. Hence it is not transitive.

Hence the given relation A is reflexive, but not symmetric and transitive.