CIRCLES CALCULATE AREA CIRCUMFERENCE RADIUS AND DIAMETER

Radius :

The radius is a line segment with one end point at the center and the other end on the circle. It is denoted by ‘r’.

Diameter :

Diameter is a chord passing through the center of the circle. It is denoted by ‘d’.

The diameter is the longest chord. It is twice the radius.(i.e. d = 2r)

Circumference :

Can we find the distance covered by an athlete if he takes two rounds on a circular track. Since it is a circular track, we cannot use the ruler to find out the distance.

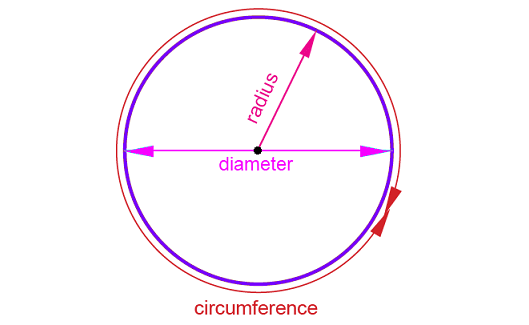
The distance around a circle is called the circumference of the circle, which is denoted by ‘C’.

Circumference of circle = 2πr

Area of circle :

The area of a circle is the number of square units inside that circle

Area of circle = πr²

Example 1 :

Find the circumference of a circle whose diameter is 21 cm.

Solution :

Diameter  =  21 cm

Radius  =  21/2 = 10.5 cm

Circumference of circle  =  2 π r

  =  2 (22/7) x 10.5

  =  44 x 1.5

  =  66 cm

Hence the circumference of circle is 66 cm.

Example 2 :

A wire of length 88 cm is bent as a circle. What is the radius of the circle?

Solution :

Length of the wire  =  circumference of the circle

2 π r  =  88 cm

2 x (22/7) x r  =  88

r  =  (88 x 7)/(2 x 22)

r  =  14 cm

Hence the radius of the circle is 14 cm

Example 3 :

The diameter of a bicycle wheel is 63 cm. How much distance will it cover in 20 revolutions?

Solution :

When a wheel makes one complete revolutions,

Distance covered in one rotation = Circumference of wheel

Circumference of the wheel = 2πr units 

=  2 x (22/7) x (63/2) cm

=  22 x 9  =  198 cm

For one revolution, the distance covered = 198 cm

For 20 revolutions, the distance covered = 20 × 198 cm

=  3960 cm

=  39 m 60 cm [100 cm = 1 m]

Hence the distance covered in 20 revolution is 39 m 60 cm

Example 4 :

A scooter wheel makes 50 revolutions to cover a distance of 8800 cm. Find the radius of the wheel.

Solution :

Distance travelled 

  =  Number of revolutions/Circumference

2πr  =  8800/50

2πr  =  176

2 x (22/7) x r  =  176

r  =  176 x (7/22) x (1/2)

r  =  28 cm

Hence the radius of the wheel is 28 cm

Example 5 :

The radius of a cart wheel is 70 cm. How many revolution does it make in travelling a distance of 132 m?

Solution :

Given: r = 70 cm, Distance travelled = 132 m.

Circumference of a cart wheel = 2πr

= 2 x (22/7) x 70

= 440 cm

Distance travelled

= Number of revolutions x  Circumference

Number of revolutions

  = Distance travelled/Circumference

  =  132 m/440 cm

  =  13200/440

  =  30

Hence the number of revolution is 30.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.