CLASSICAL DEFINITION OF PROBABILITY

Let us consider a random experiment that result in a finite elementary events, which are assumed to be equally likely.

Probability is defined by the ratio between the number of favorable outcomes to the number of all possible outcomes.

Then the formula for classic definition of probability is given by

Let A be the event in a random experiment. 

Then, 

n(A)  =  Number of possible outcomes for the event A

n(S)  =  Number of all possible outcomes of the experiment.

Here "S" stands for sample space which is the set contains all possible outcomes of the random experiment. 

Then the above formula will become

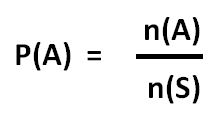
To have better understanding of the above formula, let us consider the following random experiment. 

A coin is tossed once. 

S  =  { H, T } and n(S)  =  2

Let A be the event of getting head. 

A  =  { H } and n(A)  =  1

Then,

P(A)  =  n(A) / n(S)

P(A)  =  1/2

Limitations

For this definition of probability, we are indebted to Bernoulli and Laplace. This definition is also termed as a prior definition because probability of the event A is defined on the basis of prior knowledge.

This classical definition of probability has the following demerits or limitations:

(i) It is applicable only when the total no. of events is finite.

(ii) It can be used only when the events are equally likely or equi-probable. This assumption is made well before the experiment is performed.

(iii) This definition has only a limited field of application like coin tossing, dice throwing, drawing cards etc. where the possible events are known well in advance. In the field of uncertainty or where no prior knowledge is provided, this definition is inapplicable.

In connection with classical definition of probability, we may note the following points.

Important Points

(a)  The probability of an event lies between 0 and 1, both inclusive.

That is,

0 ≤ P(A) ≤ 1

When P(A) = 0, A is known to be an impossible event and when P(A) = 1, A is known to be a sure event.

(b) Non-occurrence of event A is denoted by A’ and it is known as complimentary event of A. The event A along with its complimentary A’ forms a set of mutually exclusive and exhaustive events.

That is, 

P(A) + P(A')  =  1

P(A')  =  1 - P(A)

(c) The ratio of no. of favorable events to the no. of unfavorable events is known as odds in favor of the event A and its inverse ratio is known as odds against the event A.

Let M be the number all possible outcomes of a random experiment and Mₐ be the number favorable outcomes of the event A.

Then,

Odds in favor of A  =  M_a : (M - M_a)

Odds against A  =  (M - M_a) : M_a

Therefore, odds in favor of A and odds against A are the two ratios which are inverse to each other. 

Hence, 

Odds in favor of A x Odds against A  =  1

Example

Question :

A coin is tossed three times. What is the probability of getting :

(i)  2 heads

(ii)  at least 2 heads

Answer :

When a coin is tossed three times, first we need enumerate all the elementary events.

This can be done using 'Tree diagram' as shown below :

Hence the elementary events are HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.

That is, 

S  =  { HHH, HHT, HTH, HTT, THH, THT, TTH, TTT }

Thus the number of elementary events n(s)  =  8

(i) 2 heads :

Out of these 8 outcomes, 2 heads occur in three cases namely HHT, HTH and THH.

If we denote the occurrence of 2 heads by the event A and if assume that the coin as well as performer of the experiment is unbiased then this assumption ensures that all the eight elementary events are equally likely.

Then by the classical definition of probability, we have

P(A)  =  n(A) / n(s)

P(A)  =  3/8  

P(A)  0.375 or 37.5%

(ii) at least 2 heads :

Let B denote occurrence of at least 2 heads i.e. 2 heads or 3 heads.

Since 2 heads occur in 3 cases and 3 heads occur in only 1 case, B occurs in 3 + 1 or 4 cases.

By the classical definition of probability,

P(B)  =  4/8

P(B)  =  0.50 or 50%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.