CLASSIFYING RATIONAL NUMBERS WORKSHEET

Question 1 :

Place the following numbers in the Venn diagram. Then classify each number by indicating in which set or sets each number belongs.

0.35, -3, 75, 3/4

Question 2 :

Classify the following two numbers as rational and irrational and also explain your answer. 

5.312312312.......................

5.385164807.......................

Question 3 : 

Why is the non terminating recurring decimal

2.0343434 .........

considered to be a rational number ? Explain.

Question 4 : 

Is √26 rational or irrational number ?

Explain your answer.

Question 5 :

Can  2.0342536901 ......... be written as a fraction ? 

Detailed Answer Key

Question 1 :

Place the following numbers in the Venn diagram. Then classify each number by indicating in which set or sets each number belongs.

0.35, -3, 75, 3/4

Answer :

75 : 

The number 75 belongs in the sets of whole numbers, integers, and rational numbers.

-3 :

The number -3 belongs in the sets of integers and rational numbers.

3/4 :

The number -3/4 belongs in the set of rational numbers.

0.35 :

The number 0.35 belongs in the set of rational numbers.

Question 2 :

Classify the following two numbers as rational and irrational and also explain your answer. 

5.312312312.......................

5.385164807.......................

Answer : 

5.312312312....................... ---> Rational number

5.385164807....................... ---> Irrational number

Explanation : 

Even though 5.312312312.......... is  a non terminating decimal, there is a repeated pattern 312 in it. 

So, 5.312312312....... is non terminating recurring decimal. 

Hence, 5.312312312....... is a rational number.  

5.385164807............ is  a non terminating decimal and also there is no repeated pattern in it. 

So, 5.385164807............ is non terminating non recurring decimal. 

Hence, 5.385164807............ is an irrational number.  

Question 3 : 

Why is the non terminating recurring decimal

2.0343434 .........

considered to be a rational number ? Explain.

Solution : 

Rational number is usually expressed in the form a/b. 

So, if we can express any number in the form "a/b", the number can be considered as rational number. 

Now, let us see, how to express the number 2.0343434...... in the form a/b, say fraction. 

Step 1 : 

Let  x  =  2.0343434...........

Step 2 : 

Identify the repeated pattern

In 2.0343434..........., the repeated pattern is 34

(Because 34 is being repeated)

Step 3 :

Identify the first repeated pattern and second repeated pattern as as explained below. 

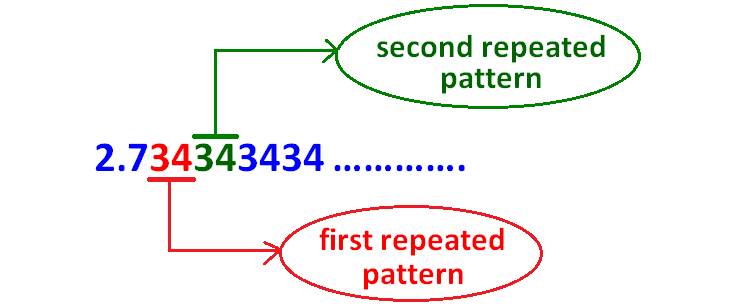
Step 4 :

Count the number of digits between the decimal point and first repeated pattern as given in the picture below. 

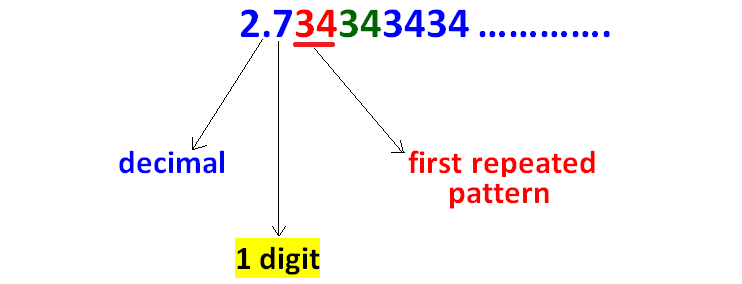
Step 5 :

Since there is 1 digit between the decimal point and the first repeated pattern, we have to multiply the given decimal by 10 as given in the picture below. 

(If there are two digits -----------> multiply by 100,

three digits -----------> multiply by 1000  and  so on )

Note :

In (1), we have only repeated patterns after the decimal.

Step 6 : 

Count the number of digits between the decimal point and second repeated pattern as given in the picture below.

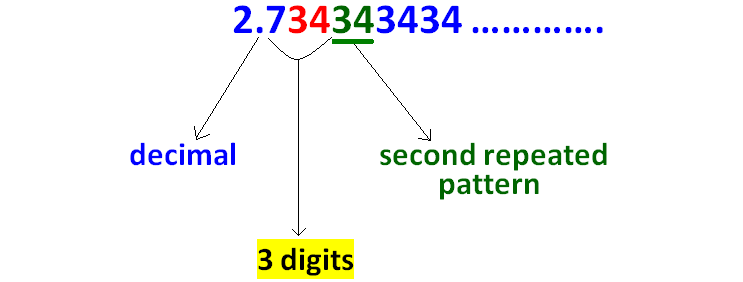
Step 7 :

Since there are 3 digits between the decimal point and the second repeated pattern, we have to multiply the given decimal by 1000 as given in the picture below. 

Note :

In (2), we have only repeated patterns after the decimal.

Step 8 :

Now, we have to subtract the result of step 5 from step 7 as given in the picture below. 

Now we got the fraction which is equal to the given decimal.

Because the given non terminating recurring decimal can be written as a fraction, it is considered to be a rational number.

Question 4 : 

Is √26 rational or irrational number ?

Explain your answer.

Solution : 

√26 is an irrational number. 

Because, when we find square root of 26, we get a non terminating non recurring decimal. 

That is, 

√26  =  5.0990195..........

Hence, √26 is an irrational number. 

Question 5 :

Can  2.0342536901 ......... be written as a fraction ? 

If yes, write the given number as a fraction. 

If no, explain why it can not be written as a fraction. 

Solution : 

No, 2.0342536901 ......... can not be written as a fraction. 

Because, 2.0342536901 ......... is a non terminating non recurring decimal. 

Note :

Only non terminating recurring decimal can be written as a fraction. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.