COMBINATIONS WORD PROBLEMS EXAMPLES

Example 1 :

Kabaddi coach has 14 players ready to play. How many different teams of 7 players could the coach put on the court?

Solution :

Number of ways of selecting 7 players out of 14 players 

=  ¹⁴C₇ 

=  14! / (14 - 7)! 7! 

=  14! / 7! 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8 ⋅ 7!)/7! 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / 7!

=  (14 ⋅ 13 ⋅ 12 ⋅ 11 ⋅ 10 ⋅ 9 ⋅ 8) / (7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2)

=  3432

Example 2 :

There are 15 persons in a party and if each 2 of them shakes hands with each other, how many handshakes happen in the party?

Solution :

Before going to look into the solution of this problem, let us create a model. 

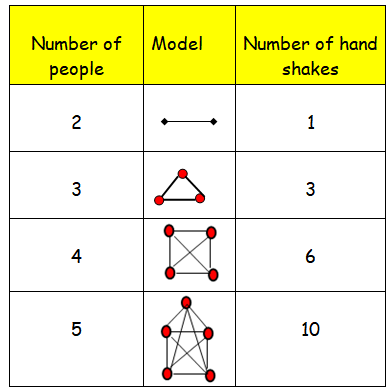
By comparing the above results, we may conclude the formula to find number of hand shakes

Number of hand shakes  =  n (n - 1)/2

Here we divide n (n - 1) by 2, because of avoiding repetition.

Number of persons in a party  =  15

Number  of hand shakes can be made  =  15 (15 - 1) / 2

  =  15 (14)/2

  =  15 (7)

  =  105

Example 3 :

How many chords can be drawn through 20 points on a circle?

Solution :

20 points lie on the circle. By joining any two points on the circle, we may draw a chord.

Number of chords can be drawn  =  ²⁰C₂

  =  20!/(20 - 2)! 2!

  =  20! / 18! 2!

  =  (20 ⋅ 19) / 2 

  =  190

Hence the required number of chords can be drawn is 190.

Example 4 :

In a parking lot one hundred , one year old cars, are parked. Out of them five are to be chosen at random for to check its pollution devices. How many different set of five cars can be chosen?

Solution :

In the given question, we have a word "different set of five cars".

So we have to use the concept combination.

Number of ways of choosing 5 cars  =  ¹⁰⁰C₅

Hence the answer is ¹⁰⁰C_5.

Example 5 :

How many ways can a team of 3 boys, 2 girls and 1 transgender be selected from 5 boys, 4 girls and 2 transgenders?

Solution :

Total number of ways  =  10 ⋅ 6 ⋅ 2

  =  120 ways

Hence the total number of ways is 120.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.