COMBINED FIGURES WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Find the perimeter and area of the following figures:
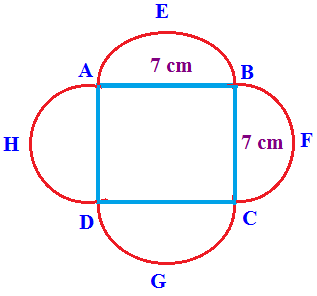
Problem 2 :
Find the area of shaded portion.
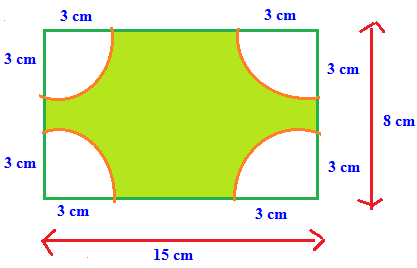
Problem 3 :
The kitchen in Mario’s Italian restaurant is 18 meters long and 12 meters wide. A square pantry is connected to the kitchen area. The pantry is 3 meters wide. What is the total area of the kitchen and pantry?
Problem 4 :
The area of triangle QTU is 6 square units, and the area of triangle RSU is 6 square units. The dimensions in the figure below are labeled in units. What is the area of triangle STU in square units?
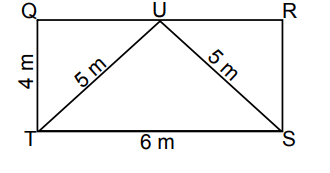
Problem 5 :
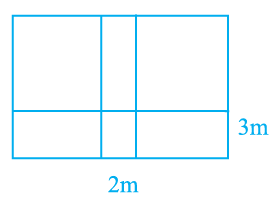
The figure below is divided into four small squares. The sides of each small square are 6 cm long. What is the area, in square centimeters, of the entire figure?
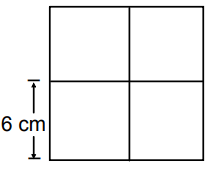
Problem 6 :
The figure is made up of a semicircle and a triangle. Find the perimeter
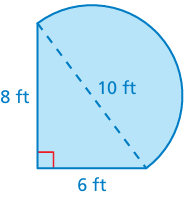
Problem 7 :
The running track is made up of a rectangle and two semicircles. Find the perimeter.
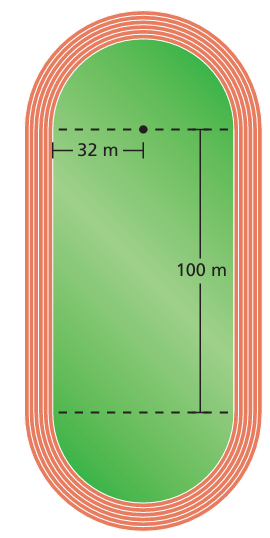
Problem 8 :
A section of land is to be fenced in for a horse pasture.
a. Find the perimeter of the pasture.
b. Fencing costs $27 per yard. How much will it cost to fence in the pasture?
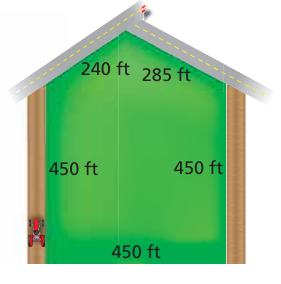
Problem 9 :
The inner circumference is 352 mm and outer is 396 mm. Find the width of circular design.

Problem 10 :
A rectangular field is 48 m long and 12 m wide. How many right triangular flower beds can be laid in this field, if sides including the right angle measure 2 m and 4 m, respectively?
Problem 11 :
A design is made up of four congruent right triangles as shown in figure. Find the area of the shaded portion.
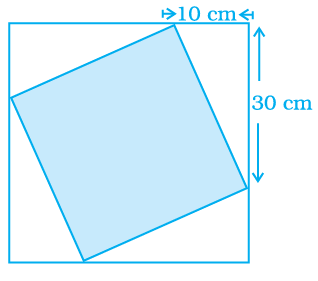
Answer Key
1) 126 cm2
2) 91.715 cm2
3) 225 square meter
4) 12 m2
5) 144 cm2
6) 63.25 square feet.
7) 400.96 square meter
8) a) 1875 ft b) $16875
9) width of the circular design is 7 mm.
10) 144 flower beds
11) 1000 square cm
Question 1 :
Find the perimeter and area of the shape shown below. (Use π ≈ 3.14).
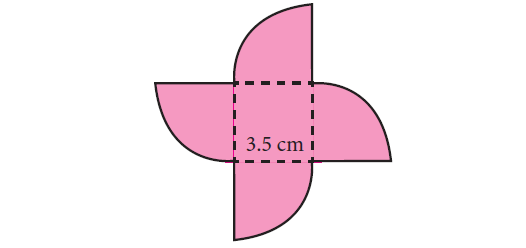
Question 2 :
Jennifer has a key-chain which is in the form of an equilateral triangle and a semicircle attached to a square of side 5 cm as shown below. Find its area. (Use π ≈ 3.14 and √3 = 1.732).

Question 3 :
A 3-fold invitation card is given with measures as shown below. Find its area.
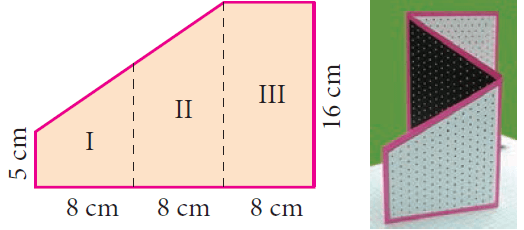
Question 4 :
A 3-fold invitation card is given with measures as shown below. Find its area.

Question 5 :
Find the area of the shaded region in the square of side 10 cm as shown below (Use π ≈ 3.14).

Question 6 :
Find the area of an irregular polygon field whose measures are as shown below.

1) 50.72 cm2 (approximately)
2) 45.64 cm2 (approximately)
3) 296 cm2
4) The total cost of the entire mat = 28 x $20 = $560.
5) 57 cm2 (approximately)
6) 226 m2
Problem 1 :
Find the area of the given polygon
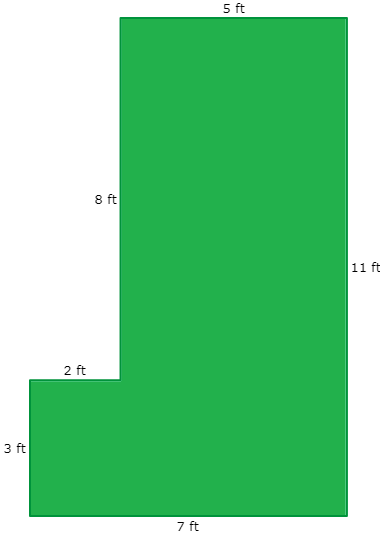
Problem 2 :
Find the area of the given polygon
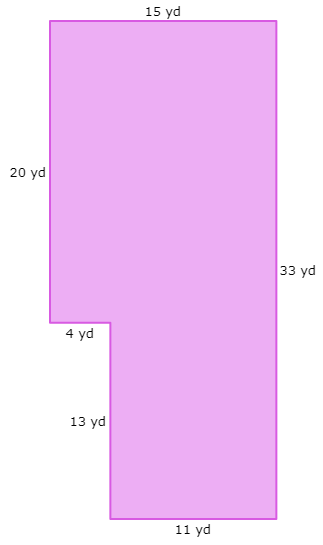
Problem 3 :
Find the area of the given polygon
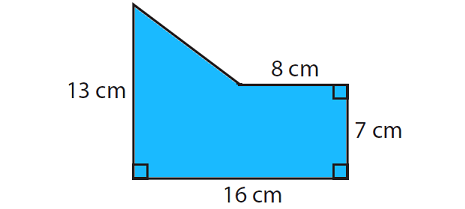
Problem 4 :
Find the area of the given polygon
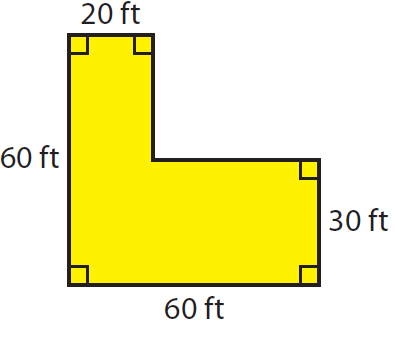
Problem 5 :
Find the area of the given polygon
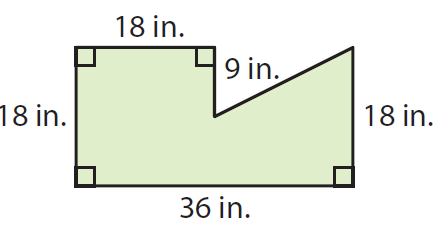
Problem 6 :
Find the area of the portion of the basketball court shown.
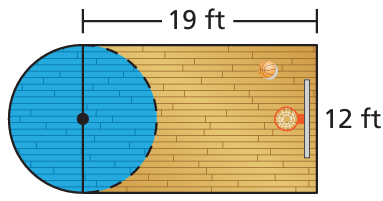
Problem 7 :
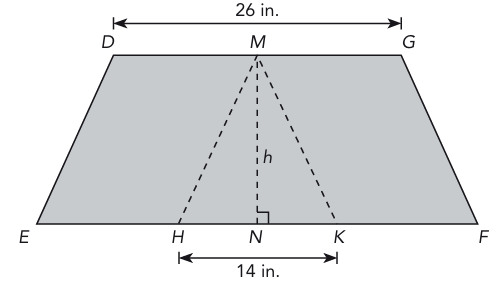
In the figure below, trapezoid DEFG is made up of triangle MHK and two identical parallelograms DEHM and MKFG. The area of triangle MHK is 105 square inches. Find the area of trapezoid DEFG.
Answer Key
1) 61 ft2
2) 443 yd2
3) 136 cm2
4) Area of the given polygon = 2400 ft2
5) 567 in2
6) 284.52 square ft
7) 495 square inches
Problem 1 :
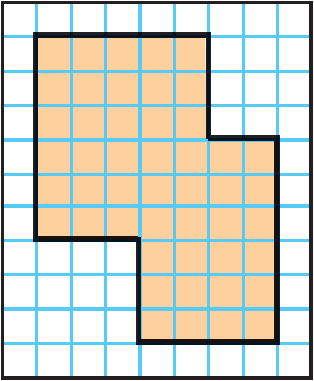
Find the area of the shaded region.
Problem 2 :
Find the area of the shaded region.

Problem 3 :
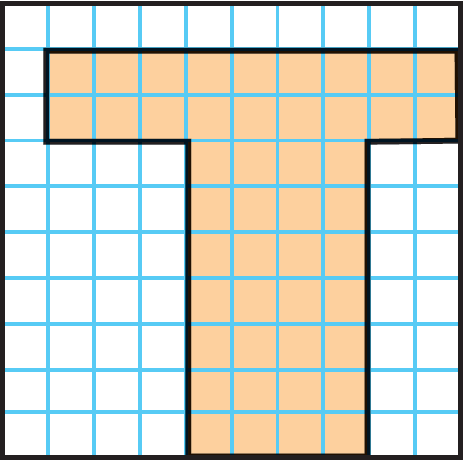
Find the area of the shaded region.
Problem 4 :
Find the area of the shaded region.

Problem 5 :
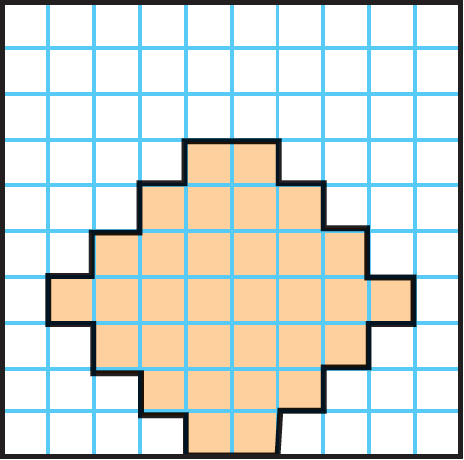
Find the area of the shaded region.
Problem 6 :
The figure is made up of a square and two semicircles. Find the perimeter.
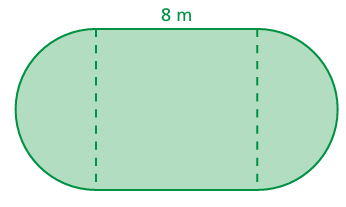
Problem 7 :
Running at 4 ft/sec, how long would it take a person to run around the baseball field?
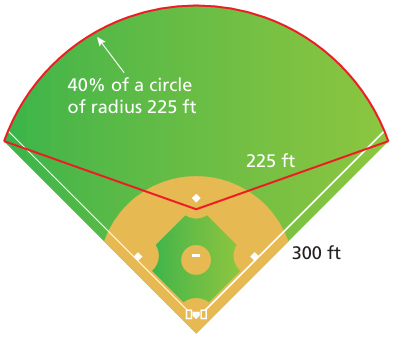
Problem 8 :
A garden is built on a rooftop. Find the perimeter of the garden.
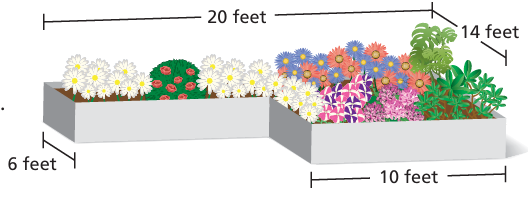
Problem 9 :
Dimensions of a painting are 60 cm × 38 cm. Find the area of the wooden frame of width 6 cm around the painting as shown
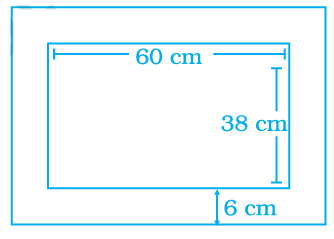
Problem 10 :
A school playground is divided by a 2 m wide path which is parallel to the width of the playground, and a 3 m wide path which is parallel to the length of the ground. If the length and width of the playground are 120 m and 80 m respectively, find the area of the remaining playground.
Answer Key
1) 48 square units
2) 17 square units
3) 46 square units
4) 32 square units
5) Count the square units inside the shaded region. The shape shows that there are 32 square units
6) 140.56 meter
7) Time taken = 5 minutes 33 seconds
8) Perimeter of the shape = 66 feet
9) Area of the frame = 720 cm2
10) area of the play ground is 9086 square meter.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


