COMBINED SHAPES
In our day-to-day life, we use infinitely many things with shapes like circle, triangle, square, rectangle, rhombus etc., don’t we? We use them separately as well as with two or three or more shapes combined together as shown in the following figures.

What do we observe from the above figures?
The shape of a glass window is like a semi-circle placed over a rectangle whereas the front – facing wall of a model house looks like a triangle over a square.
Likewise, list the shapes used to make an invitation card and a locker.
Thus, two or more plane figures joined with the sides of same measure give rise to combined shapes.
Perimeter of Combined Shapes
The perimeter of a combined shape is the sum of all the lengths of the sides that form a closed boundary.
For example, observe the figure shown below which has a square of side a units and an equilateral triangle of side a units combined together.
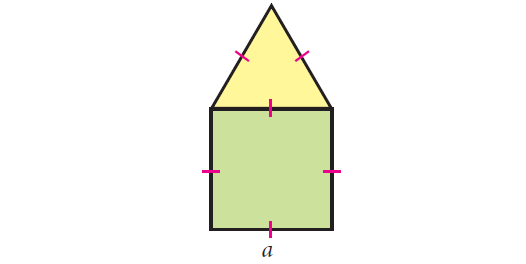
Though a square has 4 sides and an equilateral triangle has 3 sides, when they are combined together, we will have a total of only 5 sides as the boundary of the combined shape and not 7 sides. Isn’t it? So, the perimeter of the combined shape, here is 5a units.
Area of Combined Shapes
To fi nd the area of a combined shape, split the combined shape into known simpler shapes, find their area separately and then add them up. Th at is, the area of combined shapes is nothing but the sum of all the areas of the simple shapes in it.
To find the area of the figure shown above, find the area of the square and the area of the equilateral triangle separately and then add them up.
The combined shapes that we come across mostly in our day-to-day life are irregular polygons. To find the area of the given irregular polygon, we must identify the simple shapes in it, find their areas separately and then add them up.
For example, an irregular polygonal field given below can be split into known simpler shapes as under and then its area can be found.
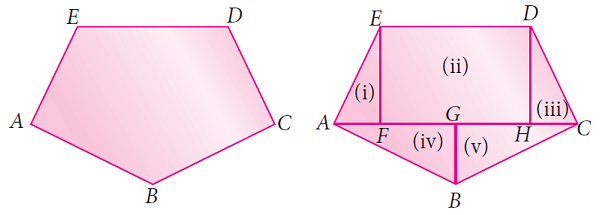
A closed plane figure formed by three or more sides is called a ‘polygon’. Based on the sides, some of the polygons are named as given below.
|
Number of Sides 3 4 5 6 7 8 9 10 |
Name of the Polygon Triangle Quadrilateral Pentagon Hexagon Heptagon Octagon Nonagon Decagon |
If all sides and all angles of a polygon are equal, then it is called as a regular polygon.
Examples :
equilateral triangle, square etc.,
Other polygons are irregular polygons.
Examples :
scalene triangle, rectangle etc.,
Example 1 :
Find the perimeter and area of the shape shown below. (Use π ≈ 3.14).
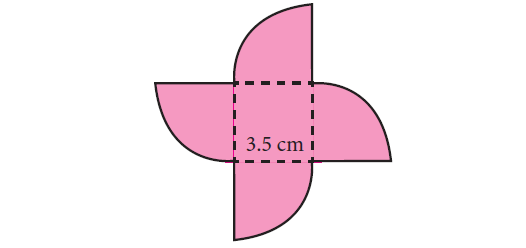
Solution :
Radius of a circular quadrant, r = 3.5 cm and side of a square, a = 3.5 cm.
The given figure is formed by the joining of 4 quadrants of a circle with each side of a square. The boundary of the given figure consists of 4 arcs and 4 radii.
Perimeter of the given combined shape :
|
= 4 x length of the arcs of the quadrant of a circle |
+ 4 x radius |
= (4 x 1/4 x 2πr) + 4r
= (1 x 2 x 3.14 x 3.5) + 4(3.5)
= 21.98 + 14
= 35.98 cm (approximately)
Area of the given combined shape :
|
= area of the square |
+ 4 x area of the quadrants of the circle |
= a2 + (4 x 1/4 x πr2)
= (3.5 x 3.5) + (1 x 3.14 x 3.5 x 3.5)
= 12.25 + 38.465
= 50.715
= 50.72 cm2 (approximately)
Example 2 :
Jennifer has a key-chain which is in the form of an equilateral triangle and a semicircle attached to a square of side 5 cm as shown below. Find its area. (Use π ≈ 3.14 and √3 = 1.732).

Solution :
Side of the square = 5 cm
Diameter of the semi-circle = 5 cm ⇒ Radius = 2.5 cm
Side of the equilateral triangle = 5 cm
Area of the key-chain :
= area of the semi circle
+ area of the square
+ area of the equilateral triangle
= (1/2)πr2 + a2 + (√3/4)a2
= (0.5 x 3.14 x 2.5 x 2.5) + (5 x 5) + [(1.732/4) x 5 x 5]
= 9.8125 + 25 + 10.825
= 45.64 cm2 (approximately)
Example 3 :
A 3-fold invitation card is given with measures as shown below. Find its area.
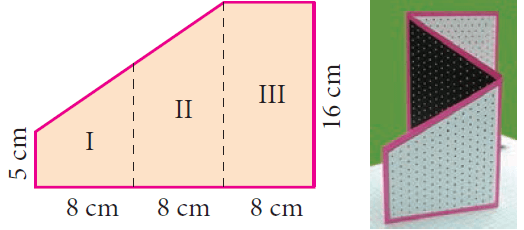
Solution :
Figures I and II are trapeziums separately as well as combinedly.
The parallel sides of the combined trapezium (I and II) are 5 cm and 16 cm and its height, h = 8 + 8 = 16 cm, length of the rectangle (III) = 16 cm and its breadth = 8 cm.
Area of the combined invitation card :
= area of the combined trapezium + area of the rectangle
= (1/2) x h x (a + b) + l x w
= 0.5 x 16 x (5 + 16) + 16 x 8
= 8 x 21 + 128
= 168 + 128
= 296 cm2
Example 4 :
Jacob wants to buy a floor mat for his kitchen at home as shown below. If the cost of the mat is $20 per square foot, what will be the cost of the entire mat?

Solution :
The mat given in the figure can be split into two rectangles as follows :

Area of the entire mat :
= area of the I rectangle + area of the II rectangle
= l1 x w1 + l2 x w2
= 5 x 2 + 9 x 2
= 10 + 18
= 28 ft2
Cost per square foot = $20.
The total cost of the entire mat = 28 x $20 = $560.
Example 5 :
Find the area of the shaded region in the square of side 10 cm as shown below (Use π ≈ 3.14).

Solution :
Mark the unshaded parts of the given figure as I, II, III and IV

Area of the I and III parts :
= Area of the square – Area of 2 semicircles
= a2 - 2 x (1/2) x πr2
= 10 x 10 - 2 x 0.5 x 3.14 x 5 x 5
= 100 - 78.5
= 21.5 cm2
Similarly, the area of the II and IV parts = 21.5 cm2.
Area of the unshaded parts (I, II, III and IV) :
= 2 x 21.5
= 43 cm2 (approximately)
Area of the shaded part :
= area of the square – area of the unshaded parts
= 100 – 43
= 57 cm2 (approximately)
Example 6 :
Find the area of an irregular polygon field whose measures are as shown below.

Solution :
The given field has four triangles (I, III, IV and V) and a trapezium.
Area of triangle (I) :
= (1/2) x b x h
= 0.5 x 5 x 6
= 15 m2
Area of trapezoid (II) :
= (1/2) x h x (a + b)
= 0.5 x 13 x (6 + 4)
= 0.5 x 13 x 10
= 65 m2
Area of triangle (III) :
= (1/2) x b x h
= 0.5 x 8 x 4
= 16 m2
Area of triangle (IV) :
= (1/2) x b x h
= 0.5 x 13 x 10
= 65 m2
Area of triangle (V) :
= (1/2) x b h
= 0.5 x 13 x 10
= 65 m2
The total area of the field :
= 15 + 65 + 16 + 65 + 65
= 226 m2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Logarithmic Derivative Problems and Solutions
Apr 16, 25 09:25 PM
Logarithmic Derivative Problems and Solutions -
Digital SAT Math Problems and Solutions (Part - 145)
Apr 16, 25 12:35 PM
Digital SAT Math Problems and Solutions (Part - 145) -
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144)

