COMMON FACTORS

Consider the numbers 45 and 60. You can use divisibility tests to find the factors of 45 and 60.

The factors of 45 are

1, 3, 5, 9, 15 and 45

The factors of 60 are

1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60

Here, the common factors of 45 and 60 are 1, 3, 5 and 15.

As factors of a number are finite, we can think of the greatest common factor of numbers, shortly denoted as GCF.

The greatest common factor of 45 and 60 is 15.

In other words, the greatest number that can divide both 45 and 60 evenly is 15. 

If you need to find the greatest common factor of two or more numbers, it is useful first to find the prime factorizations of the numbers.   

Prime factorization

Step 1 : 

Divide the number by the smallest prime number which will divide evenly. 

(Prime number is a number that can be divided evenly by itself and 1)

The first ten prime numbers are : 

2, 3, 5, 7, 11, 13, 17, 19, 23, 29

Step 2 :

Divide the quotient by a prime number again. If possible, or the next prime number that is a factor. Keep going until the quotient is prime.

Example : 

Find the prime factors of 36. 

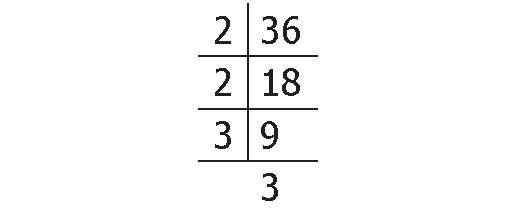
So, the number 36 can be expressed as : 

36  =  2 x 2 x 3 x 3  =  2² x 3²

Greatest Common Factor (GCF)

Step 1 :

Find the prime factorizations of each number. 

Step 2 : 

Write the product of the smallest power of each factor that appears in both prime factorizations. 

Example : 

Find the GCF of 216 and 300. 

216  =  2 x 2 x 2 x 3 x 3 x 3  =  2³ x 3³

300  =  2 x 2 x 3 x 5 x 5  =  2² x 3 x 5²

The only prime factors of these numbers that appear in both are 2 and 3. 

The smallest power of 2 that appears is 2² and the smallest power of 3 is just 3. 

Therefore, the GCF of 216 and 300 is 

=  2² x 3

=  4 x 3

=  12

Co-Primes or Relatively Prime or Mutually Prime

If the greatest common factor of two numbers is 1, then the two numbers are said to be co-primes or relatively prime or mutually prime.

Here, the two numbers can both be primes as (3, 11) or both can be composites as (16, 35) or one can be a prime and other a composite as (7, 14).

Solved Problems

Problem 1 : 

(a) List all the factors of 10

(b) List all the factors of 15

(c) Write down all the common factors of 10 and 15. 

Solution :

(a) The factors of 10 are

1, 2, 5 and 10

(b) The factors of 15 are

1, 3, 5 and 15

(c) The common factors of 10 and 15 are 

1 and 5

Problem 2 : 

(a) List all the factors of 12

(b) List all the factors of 18

(c) Write down all the common factors of 12 and 18. 

Solution : 

(a) The factors of 12 are

1, 2, 3, 4, 6 and 12

(b) The factors of 18 are

1, 2, 3, 6 and 18

(c) The common factors of 12 and 18 are 

1, 2, 3 and 6

Problem 3 : 

Write the common factors of 9, 36 and 45. 

Factors of 9 :  

1, 2, 3, 9

Factors of 36 :

1, 2, 3, 4, 6, 12, 18, 36

Factors of 45 :

1, 3, 5, 9, 15, 45

the common factors of 9, 36 and 45 are

1 and 3

Problem 4 : 

Find the GCF of 72 and 96. 

72  =  2 x 2 x 2 x 3 x 3  =  2³ x 3²

96  =  2 x 2 x 2 x 2 x 2 x 3  =  2⁴ x 3

We find 2 and 3 as common prime factors of 72 and 96.

The smallest power of 2 that appears is 2³ and the smallest power of 3 is just 3. 

Therefore, the GCF of 72 and 96 is 

=  2³ x 3

=  8 x 3

=  24

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.