COMMUTATIVE PROPERTY OF SET

Example 1 :

A = {-10, 0, 1, 9, 2, 4, 5} and B = {- 1,- 2, 5, 6, 2, 3, 4}, for the sets A and B, verify that

(i) Set union is commutative. Also verify it by using Venn diagram.

(ii) Set intersection is commutative. Also verify it by using Venn diagram.

Solution :

Commutative property :

(i) A u B = B u A

(ii) A n B = B n A

(i) A = {-10, 0, 1, 9, 2, 4, 5} and B = {- 1, -2, 5, 6, 2, 3, 4}

A u B = {-10, 0, 1, 9, 2, 4, 5} u {-1,-2, 5, 6, 2, 3, 4} 

= {-10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ----(1)

B u A = {-1, -2, 5, 6, 2, 3, 4} u {-10, 0, 1, 9, 2, 4, 5}

=  {-10, -2, -1, 0, 1, 2, 3, 4, 5, 6, 9} ----(2)

(1) = (2)

Verifying in Venn diagram :

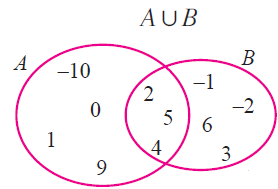
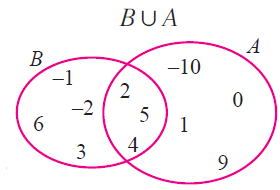
(ii) A = {-10, 0, 1, 9, 2, 4, 5} and B = {-1,-2, 5, 6, 2, 3, 4}

A n B = {-10, 0, 1, 9, 2, 4, 5} n {-1,-2, 5, 6, 2, 3, 4}

= { 2, 4, 5 } ----(3)

B n A = {-1,-2, 5, 6, 2, 3, 4} n {-10, 0, 1, 9, 2, 4, 5}

= { 2, 4, 5 } ----(4)

(3) = (4)

Verifying in Venn diagram :

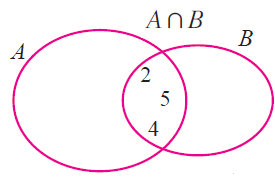
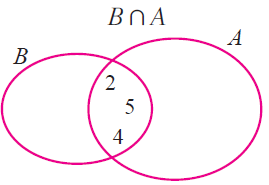
Example 2 :

A = {1, 2, 3, 4, 5} and B = {3, 4, 5, 6}, for the sets A and B, verify that

(i) set union is commutative. 

(ii) set intersection is commutative. 

Solution :

Commutative property :

(i) A u B = B u A

(ii) A n B = B n A

(i) A = {1, 2, 3, 4, 5} and B = {3, 4, 5, 6} 

A u B = {1, 2, 3, 4, 5} u {3, 4, 5, 6} 

= {1, 2, 3, 4, 5, 6} ----(5)

B u A = {3, 4, 5, 6} u {1, 2, 3,  4, 5}

= {1, 2, 3, 4, 5, 6} ----(6)

(5) = (6)

(i) A = {1, 2, 3,  4, 5} and B = {3, 4, 5, 6} 

A n B = {1, 2, 3, 4, 5} n {3, 4, 5, 6} 

= {3, 4, 5} ----(7)

B n A =  {3, 4, 5, 6} U {1, 2, 3,  4, 5}

= {3, 4, 5} ----(8)

(7) = (8)

Example 3 :

In a class of 50 students, 35 opted for Mathematics and 37 opted for Commerce. The number of such students who opted for both Mathematics and Commerce are 

a)  13    b)  15   c)  22   d)  28

Solution :

Total number of students = 50

Let A and B be number of students who opted for Math and Commerce respectively.

Number of students opted for Mathematics = 35

Number of students opted for Commerce = 37

Let A n B be the number of students who opted for Math and Commerce.

n(A U B) = n(A) + n(B) - n(A n B)

50 = 35 + 37 - n(A n B)

n(A n B) = 35 + 37 - 50

= 72 - 50

= 22

So, number of students who opted for both Math and Commerce is 22.

Example 4 :

In a class of 80 students, 35% students can play cricket, 45% students can pay only tennis and the remaining students can  play both games. In all how many students can lay cricket ?

a)  55      b)  44    c)  36     d)  28

Solution :

Total number of students in the class = 80

Let A and B be the number of students play cricket and tennis.

n(A n B bar) = 35% ==> 0.35(80) ==> 28

n(B n A bar) = 45% ==> 0.45 (80) ==> 36

n(A U B) = 80

Let n(A n B) = x

n(A n B bar) = n(A) - n(AnB)

28 = n(A) - x

n(A) = 28 + x

n(B n A bar) = n(B) - n(AnB)

36 = n(B) - x

n(B) = 36 + x

n(AUB) = n(A) + n(B) - n(AnB)

28 + x + 36 + x - x = 80

64 + x = 80

x = 80 - 64

x = 16

So, the number of students who play cricket is 16.

Example 5 :

If Set A is any set subset of an Universal Set U then A ∩ U = A

Solution :

For example,

If Set U = {1, 2, 3, 4, 5, 6, 7} and Set A = {1, 2, 3, 4}

then A ∩ U = {1, 2, 3 ,4, 5, 6, 7} ∩ {1, 2, 3, 4}

= {1, 2, 3, 4}

= A

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.