COMPARING A GRAPH AND A DESCRIPTION WORKSHEET

Problem 1 :

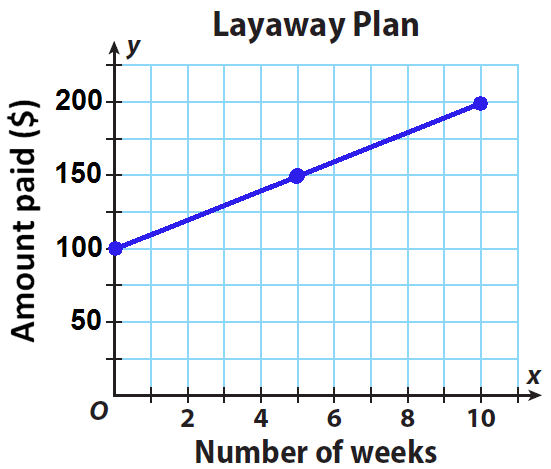
Jose wants to buy a new game system that costs $200. He does not have enough money to buy it today, so he compares layaway plans at different stores. Store A requires an initial payment of $60 and weekly payments of $20 until the balance is paid in full. The plan at Store B is shown on the graph.

Problem 2 :

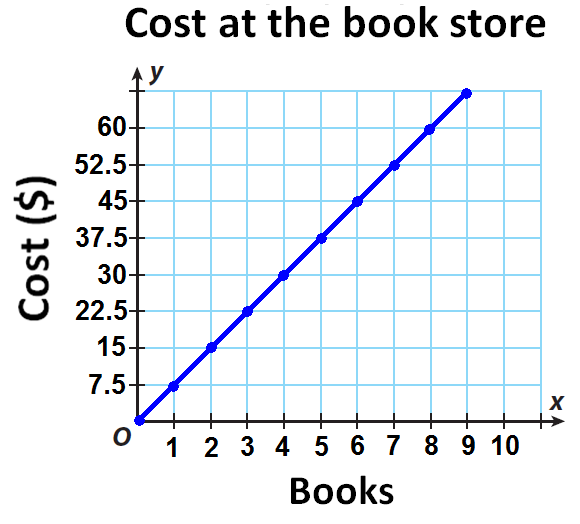
Alex is choosing between buying books at the bookstore or buying online versions of the books for his tablet. To buy books online, he has to pay an one time payment of $1.50 for registration and $6.95 per book. The cost of buying the books at the bookstore is shown in the graph. Which method of buying books is more expensive if Quentin wants to buy 6 books ?

Detailed Answer Key

Problem 1 :

Jose wants to buy a new game system that costs $200. He does not have enough money to buy it today, so he compares layaway plans at different stores. Store A requires an initial payment of $60 and weekly payments of $20 until the balance is paid in full. The plan at Store B is shown on the graph.

Based on the information given above, find which store allows Jose to pay for the game system faster. 

Solution : 

Step 1 :

To find which store allows Jose to pay for the game system faster, let us have the deals offered by store A and B as equations.

Write an equation in slope-intercept form for Store A’s layaway plan.

Let x represent number of weeks and y represent the total money to be paid.

y  =  20x + 60

Step 2 :

Write an equation in slope-intercept form for Store B’s layaway plan.

Let x represent number of weeks and y represent the total money to be paid. 

From the graph, y - intercept is 100 and the slope is 10

y  =  10x + 100

Step 3 :

In both the stores A and B, find the value of "x" (no. of weeks) for y = $200 (Total money to be paid). 

The total amount $200 is completed in 7 weeks in store A and in 10 weeks in store B. 

So, store A allows Jose to pay for the game system faster

Problem 2 :

Alex is choosing between buying books at the bookstore or buying online versions of the books for his tablet. To buy books online, he has to pay an one time payment of $1.50 for registration and $6.95 per book. The cost of buying the books at the bookstore is shown in the graph. Which method of buying books is more expensive if Quentin wants to buy 6 books ?

Solution : 

Step 1 :

To find which method of buying books is more expensive if Quentin wants to buy 6 books, let us have both the methods as equations.

Write an equation in slope-intercept form for buying books online. 

Let x represent number of books and y represent the cost for x number of books.

y  =  6.95x + 1.50

Step 2 :

Write an equation in slope-intercept form for buying books at the book store. 

Let x represent number of books and y represent the cost for x number of books.

From the graph, y - intercept is 0 and the slope is 7.5

y  =  7.5x + 0

y  =  7.5x

Step 3 :

In both the methods, find the value of "y" (cost) for x = 6 (number of books). 

So, buying books at the book store is expensive. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.