COMPARING RADICALS

Radicals of same order : 

³√3, ³√6, ³√10

Radicals of different orders : 

√5, ³√4, ⁴√9

Radicand : 

The value inside the radical sign.

Example : 

In √x, x is the radicand.

Comparing Radicals of Same Order

To compare two or more radicals of same order, we have to compare the radicands.

For example, let us consider the following two radicals of same order. 

³√9 and ³√7

In the above two radicals, the radicands are 9 and 7.

And also, 

9  >  7

Then

³√9  >  ³√7

Comparing Radicals of Different Orders

To compare two or more radicals of different orders, first we have to convert them into radicals of different orders. Then, we have compare the radicands. 

Using the least common multiple of the different orders given, we can convert the radicals of different orders into radicals of same order. 

For example, let us consider the following radicals of different orders.

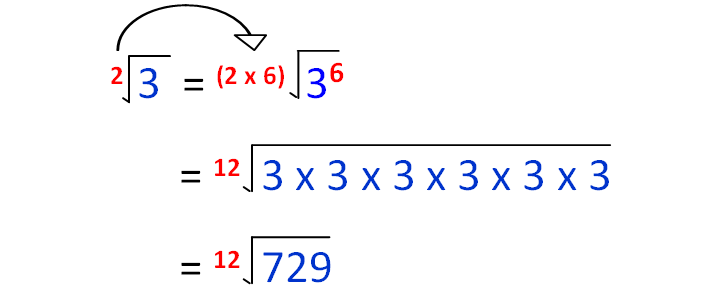
 √3, ³√2 and ⁴√4

The orders of the above radicals are 2, 3 and 4. 

Thee least common multiple of (2, 3 and 4) is 12.

So, we have to make the order of each radical as 12. 

Then, 

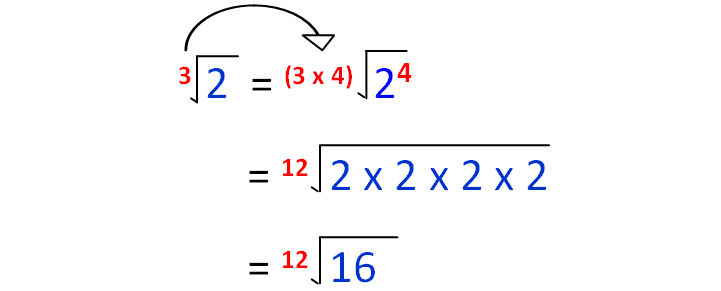
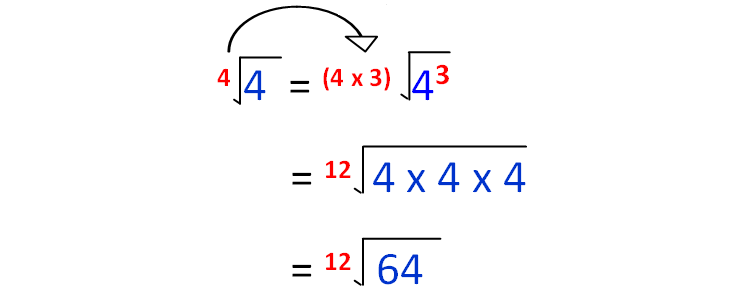
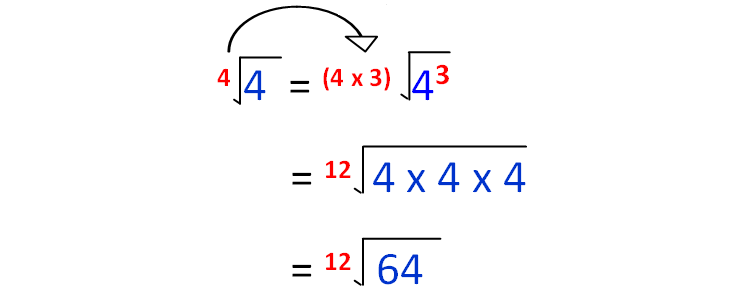
From the above calculations,  

Now, all radicals are expressed in the same order. 

Compare the radicands :

729  >  64  >  16

Then, 

¹²√729  >  ¹²√64  >  ¹²√16

Therefore, 

 √3  >  ⁴√4  >  ³√2

Comparing Radicals with Same Radicand

If two radicals of different orders have the same radicand, then the radical with the smaller order will be greater in value.  

For example, 

³√5  >  ⁵√5 

Practice Questions

Question 1 :

Which is greater  ? 

√4 or √6

Answer :

The above two radicals have the same  order (i.e., 2).

To compare the above radicals, we have to compare the radicands 4 and 6. 

Clearly 6 is greater than 4. 

So, √6 is greater than √4. 

That is, 

√6  >  √4

Question 2 :

Which is greater ? 

√2 or ³√3

Answer :

The above two radicals have different orders. The are 2 and 3.

Using the least common multiple of the orders 2 and 3, we can convert them into radicals of same order. 

Least common multiple of (2 and 3) is 6.

Then, 

√2  =  ^2x3√(2³)  =  ⁶√8

³√3  =  ^3x2√(3²)  =  ⁶√9

Now, the given two radicals are expressed in the same order. 

Compare the radicands :

9  >  8

Then, 

⁶√9  >  ⁶√8

Therefore, 

 ³√3  >  √2

Question 3 :

Which is greater ? 

⁴√3 or ⁶√4

Answer :

The above two radicals have different orders. The are 4 and 6.

Using the least common multiple of the orders 4 and 6, we can convert them into radicals of same order. 

Least common multiple of (4 and 6) is 12.

Then, 

⁴√3  =  ^4x3√(3³)  =  ¹²√27

⁶√4  =  ^6x2√(4²)  =  ¹²√16

Now, the given two radicals are expressed in the same order. 

Compare the radicands :

27  >  16

Then, 

¹²√27  >  ¹²√16

Therefore, 

⁴√3  >  ⁶√4

Question 4 :

Which is greater ? 

⁴√4 or ⁵√5

Answer :

The above two radicals have different orders. The are 4 and 5.

Using the least common multiple of the orders 4 and 5, we can convert them into surds of same order. 

Least common multiple of (4 and 5) is 20.

Then, 

⁴√4  =  ^4x5√(4⁵)  =  ²⁰√1024

⁵√5  =  ^5x4√(5⁴)  =  ²⁰√625

Now, the given two radicals are expressed in the same order. 

Compare the radicands :

1024  >  625

Then, 

²⁰√1024  >  ²⁰√625

Therefore, 

⁴√4  >  ⁵√5

Question 5 :

Which is greater ? 

⁷√25 or ⁵√25

Answer :

The above two radicals have different orders with the same radicand.

Then, the radical with the smaller order will be greater in value.

Therefore, ⁵√25 is greater than ⁷√25. 

That is, 

⁵√25  >  ⁷√25

Question 6 :

Arrange the following radicals in ascending order :

³√4, ⁶√5  and ⁴√6

Answer :

The orders of the above radicals are 3, 6 and 4. 

The least common multiple of (3, 6 and 4) is 12.

So, we have to make the order of each radical as 12. 

Then, 

³√4  =  ^3x4√(4⁴)  =  ¹²√256

⁶√5  =  ^6x2√(5²)  =  ¹²√25

⁴√6  =  ^4x3√(6³)  =  ¹²√216

Now, the given two radicals are expressed in the same order. 

Arrange the radicands in ascending order : 

25, 216, 256  

Then, 

¹²√25, ¹²√216, ¹²√256

Therefore, the ascending order of the given radicals is 

⁶√5, ⁴√6, ³√4

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.