COMPARING RATIOS WORD PROBLEMS

Problem 1 :

Anna’s recipe for lemonade calls for 2 cups of lemonade concentrate and 3 cups of water. Bailey’s recipe calls for 3 cups of lemonade concentrate and 5 cups of water. Whose recipe makes stronger lemonade ?  How do you know ?

Solution :

Anna’s recipe :

2 cups of lemonade and 3 cups of water.

So, the ratio is 2 : 3.

Let us write equivalent ratios to the ratio 2 : 3.

Bailey’s recipe :

3 cups of lemonade and 5 cups of water.

So, the ratio is 3 : 5.

Let us write equivalent ratios to the ratio 3 : 5.

Find two columns, one in each table, in which the amount of water is the same. Circle those two columns.

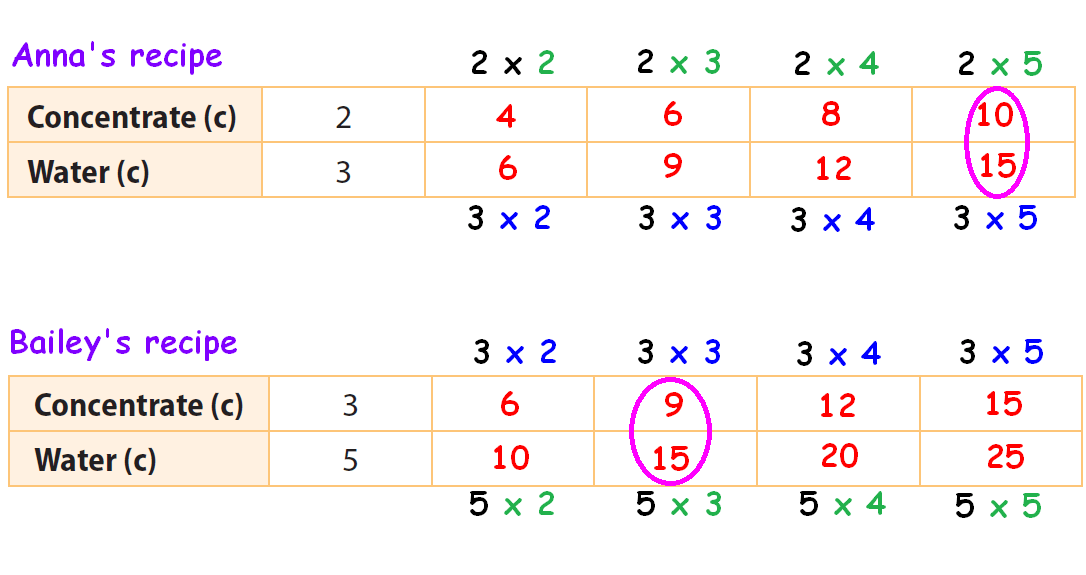
From the circled columns, we get two ratios. 

They are, 

10 : 15 and 9 : 15

In these two ratios, the second quantity (water) is same. 

So, we have to compare the first quantity (Lemonade).

The first quantity (10) in the first ratio is more than the first quantity (9) in the second ratio. 

When the amount of water is same (15) in both recipes, Anna's recipe has more quantity of lemonade concentrate.

Therefore, Anna's recipe has stronger lemonade. 

Problem 2 :

There are two alloys A and B, both are made up of gold and copper. The ratio between gold and copper in each alloy is given below.

Alloy A (G : C)----> 2 1/3  :  3  1/3

Alloy B (G : C) ----> 3.6 : 4.8

In which alloy do we have more gold ?

Solution :

To know the alloy in which we have more gold, we have to compare the given two ratios.

To compare two ratios, both the terms of the ratio must be integers. 

Let us convert the terms of the first ratio into integers. 

2 1/3  :  3  1/3  =  (7/3) : (10/3)

2 1/3  :  3  1/3  =  7 : 10 ------> multiplied by 3 

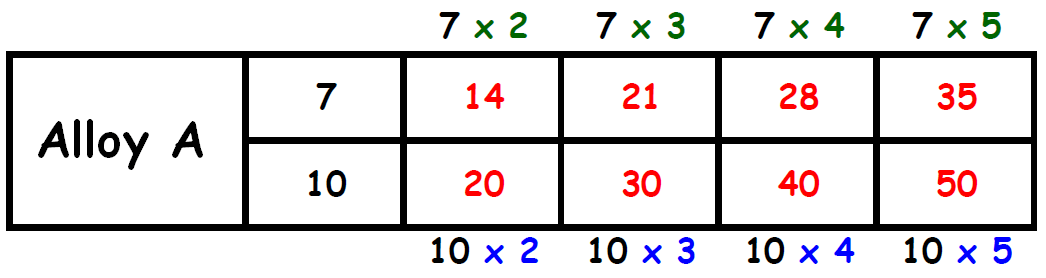
Let us write equivalent ratios to the ratio 7 : 10

Let us convert the terms of the second ratio into integers. 

3.6 : 4.8  =  36 : 48 ------> multiplied by 10 

3.6 : 4.8  =  3 : 4 ------> divided by 12 

Let us write equivalent ratios to the ratio 3 : 4

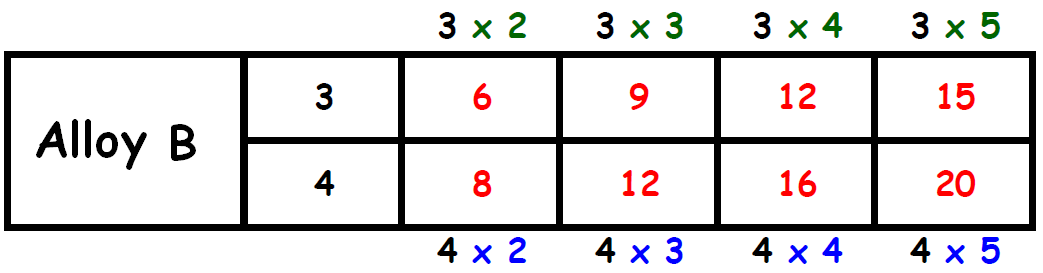
Find two columns, one in each table, in which the the second term is same. Circle those two columns.

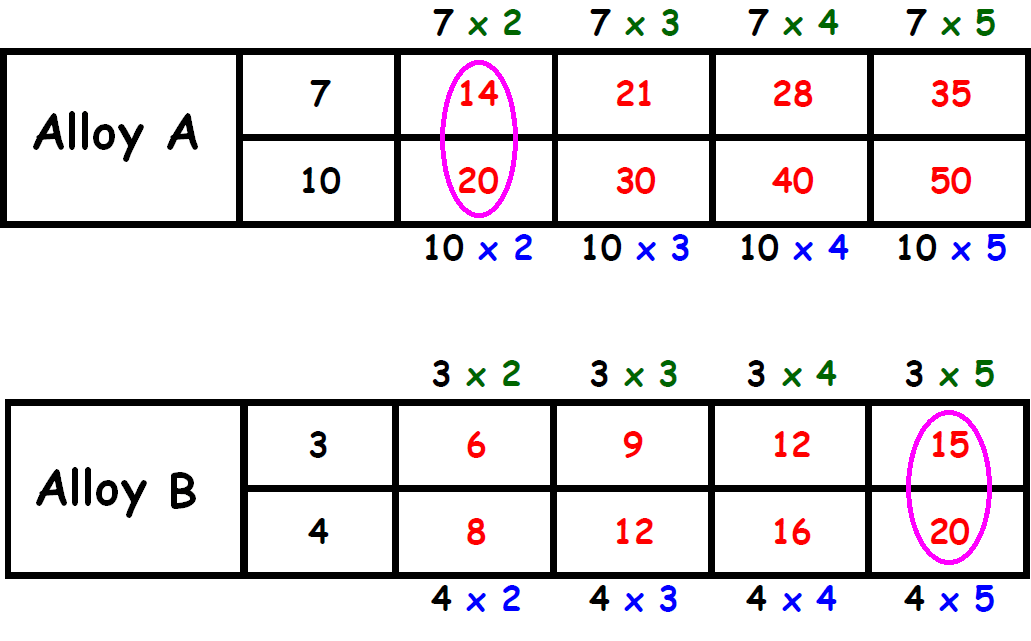
From the circled columns, we get two ratios. 

They are, 

14 : 20 and 15 : 20

In these two ratios, the second quantity (copper) is same. 

So, we have to compare the first quantity (gold).

The first quantity (15) in the second ratio is more than the first quantity (14) in the first ratio. 

When the quantity of copper is same (20) in both the alloys, Alloy A has more quantity of gold. 

Therefore, we have more gold in alloy A. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.