COMPARING TWO SETS OF DATA USING MEAN AND STANDARD DEVIATION

Example 1 :

The mean and standard deviation of marks obtained by 40 students of a class in three subjects Mathematics, Science and Social Science are given below

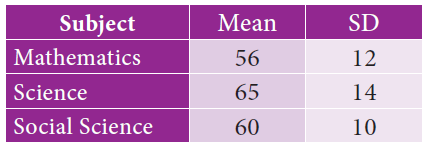
Which of the three subjects shows highest variation and which shows lowest variation in marks?

Solution :

The highest variation is in the subject Science and lowest variation is in the subject Social science

Example 2 :

The temperature of two cities A and B in a winter season are given below.

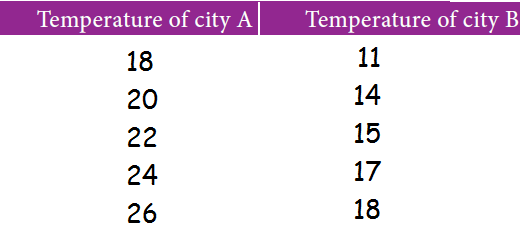
Find which city is more consistent in temperature changes?

Solution :

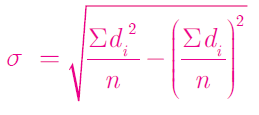
Temperature of city A :

Σd²/n  =  40/5  =  8

(Σd/n)²  =  (0)²  =  0

σ  =  √(8 - 0)

  =  √8

σ  =  2.82

Mean (x̄)  =  (18 + 20 + 22 + 24 + 26)/ 5

  = 110/5

x̄  = 22

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

x̄  =  22, σ  =  2.82

C.V  =  (2.82/22) ⋅ 100%

C.V  =  0.1281⋅ 100%

C.V  =  12.81%

Temperature of city B :

Σd²/n  =  30/5  =  6

(Σd/n)²  =  0 

σ  =  √(6 - 0)

  =  √6

σ  =  2.44

x̄  =  Σx/n 

=  (11+14+15+17+18)/5

x̄  =  75/5

x̄  =  15

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

C.V  =  (2.44/15) ⋅ 100%

C.V  =  (244/1500) ⋅ 100%

C.V  =  0.1626 ⋅ 100%

C.V  =  16.26%

So, city A is more consistent.

Example 3 :

The following table gives the values of mean and variance of heights and weights of the 10th standard students of a school.

Which is more varying than the other ?

Solution :

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

Finding coefficient of variation for first data :

Mean = 155 cm, variance σ² = 72.25

σ = √72.25 ==> 8.5

C.V₁ =  (8.5/155) ⋅ 100%

= 0.054 x 100%

= 5.48%

Finding coefficient of variation for second data :

Mean = 46.50,  variance σ² = 28.09

σ = √28.09 ==> 5.3

C.V₁ =  (5.3/46.50) ⋅ 100%

= 0.1139 x 100%

= 11.39%

Height is varying more, then height is more consistent.

Example 4 :

Which of two subjects shows the highest variability in marks and which shows the lowest.

Solution :

Finding coefficient for Mathematics :

Mean = 42,  standard deviation σ = 12

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

C.V₁ =  (12/42) ⋅ 100%

= 0.2857 x 100%

= 28.57%

Finding coefficient for Physics :

Mean = 42,  standard deviation σ = 15

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

C.V₁ =  (12/15) ⋅ 100%

= 0.8 x 100%

= 80%

The subject Physic has highest variability and Mathematics has lowest variability.

Example 5 :

If two data’s A and B have same mean 25 each and their standard deviations are 4.5 and 6.7 respectively. Which data A or B is more variable.

Solution :

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

For data A :

mean = 25, standard deviation = 4.5

(C.V) =  (4.5/25) ⋅ 100%

= 0.18 x 100%

= 18%

For data A :

mean = 25, standard deviation = 6.7

(C.V) =  (6.7/25) ⋅ 100%

= 0.268 x 100%

= 26.8%

Data set B is more variable.

Example 6 :

If co-efficient of variation of distribution is 75 and standard deviation is 2% , the mean is _____

Solution :

Coefficient of variation = 75

standard deviation = 2% = 0.02

Coefficient of variation (C.V) =  (σ/x̄) ⋅ 100%

75 =  (0.02/x̄) ⋅ 100%

75 = 0.02/x̄

x̄ = 0.02/75

x̄ = 2.67(approximately)

So, the required mean is 2.67 (approximately).

Example 7 :

The following is the record of goals scored by team A in football session :

For the team B , mean number of goals scored per match was 2 with a standard deviation 1.25 goals. Find which team may be considered more consistent ?

Solution :

For team A :

Mean x̄ = Σfx / Σf

= [0(1) + 1(9) + 2(7) + 3(5) + 4(3)] / (1 + 9 + 7 + 5 + 3)

= (0 + 9 + 14 + 15 + 12) / 25

= 50/25

= 2

Finding standard deviation :

Standard deviation = √(Σfd² / Σf)

Σfd² = 4 + 9 + 0 + 5 + 12

= 30

Σf = 1 + 9 + 7 + 5 + 3

= 25

σ = √(30/25)

= √1.2

σ = 1.09

Coefficient of variation for team A :

(C.V) =  (σ/x̄) ⋅ 100%

= (1.09/2) x 100%

= 54.5%

For team B :

Mean = 2, standard deviation = 1.25

Coefficient of variation for team B :

(C.V) =  (σ/x̄) ⋅ 100%

= (1.25/2) x 100%

= 62.5%

So, team B is more consistent.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.