COMPLEMENTARY AND SUPPLEMENTARY ANGLES WORD PROBLEMS

In this section, you will learn how to solve word problems on complementary and supplementary angles.

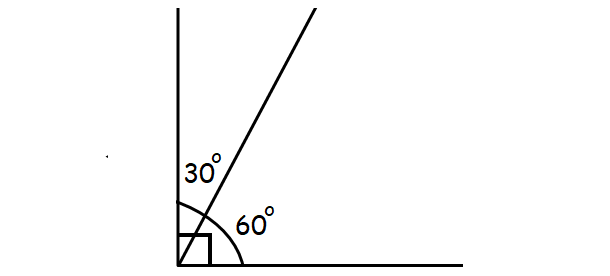
Problem 1 :

Two angles are complementary. If one of the angles is double the other angle, find the two angles.

Solution :

Let x be one of the angles.

Then the other angle is 2x.

Because x and 2x are complementary angles, we have

x + 2x = 90

3x = 90

Divide each side by 3.

x = 30

2x = 2(30) = 60

So, the two angles are 30° and 60°.

Problem 2 :

Two angles are complementary. If one angle is two times the sum of other angle and 3, find the two angles.

Solution :

Let x and y be the two angles which are complementary.

x + y = 90 ----> (1)

Given : One angle is two times the sum of other angle and 3.

x = 2(y + 3)

x = 2y + 6 ---->(2)

Now, substitute (2y + 6) for x in (1).

2y + 6 + y = 90

3y + 6 = 90

Subtract 6 from each side.

3y = 84

Divide each side by 3.

y = 28

Substitute 28 for y in (2).

x = 2(28) + 6

x = 56 + 6

x = 62

So, the two angles are 62° and 28°.

Problem 3 :

The measure of an angle is 3/4 of 60°. What is the measure of the complementary angle?

Solution :

Let x be the measure of a complementary angle required.

Given : The measure of an angle is 3/4 of 60°.

3/4 ⋅ 60° = 45°

Because x and 45° are complementary angles,

x + 45 = 90

Subtract 45 from each side.

x = 45

So, the measure of the complementary angle is 45°.

Problem 4 :

Two angles are supplementary. If one angle is 36° less than twice of the other angle, find the two angles.

Solution :

Let x and y be the two angles which are supplementary.

x + y = 180 ---->(1)

Given : One angle is 36° less than twice of the other angle.

x = 2y - 36 ---->(2)

Now substitute (2y - 6) for x in (1),

2y - 36 + y = 180

3y - 36 = 180

Add 36 to each side.

3y = 216

Divide each side by 3.

y = 72

Now, Substitute 72 for y in (2).

x = 2(72) - 36

x = 144 - 36

x = 108

So, the two angles are 108° and 72°.

Problem 5 :

An angle and its one-half are complementary. Find the angle.

Solution :

Let x be the required angle.

Then, one-half of the angle is x/2.

Given : An angle and its one-half are complementary.

x + x/2 = 90

2x/2 + x/2 = 90

(2x + x)/2 = 90

3x/2 = 90

Multiply each side by 2.

3x = 180

Divide each side by 3.

x = 60

So, the required angle is 60°.

Problem 6 :

Two angles are supplementary. If 5 times of one angle is 10 times of the other angle. Find the two angles.

Solution :

Let x and y be the two angles which are supplementary.

x + y = 180 ----(1)

Given : 5 times of one angle is 10 times of the other angle.

5x = 10y

Divide each side by 5.

x = 2y ----(2)

Substitute 2y for x in (1).

2y + y = 180

3y = 180

Divide each side by 3.

y = 60

Substitute 60 for y in (2).

x = 2(60)

x = 120

So, the two angles are 60° and 120°.

Problem 7 :

The measure of the supplement of angle A is 40 degrees larger than twice the measure of the complement of angle of A. What is the sum in degrees, of the measures of the supplement and complement of angle A?

Solution :

Let x be the measure of angle A.

supplement of angle A = 180° - x

complement of angle A = 90° - x

Given : The measure of the supplement of angle A is 40 degrees larger than twice the measure of the complement of angle of A.

(180° - x) is 40° more than 2(90° - x)

180 - x = 2(90 - x) + 40

180 - x = 180 - 2x + 40

Subtract 180 from each side.

-x = -2x + 40

Add 2x to each side.

x = 40

Then, supplement of angle A is

= 180 - x

= 180 - 40

= 140°

Complement of angle A is

= 90 - x

= 90 - 40

= 50°

The sum of supplement and complement of angle A is

= 140° + 50°

= 190°

So, the sum of supplement and complement of angle A is 190° degrees.

Problem 8 :

Twice the complement of an angle is 24 degrees less than its supplement. What is the measure of the angle?

Solution :

Let x be the measure of angle.

supplement of angle = 180° - x

complement of angle = 90° - x

Given : Twice the complement of an angle is 24 degrees less than its supplement.

2(90° - x) is 24 degrees less than (180° - x)

2(90 - x) = (180 - x) - 24

180 - 2x = 180 - x - 24

Subtract 180 from each side.

-2x = -x - 24

Add x to each side.

-x = -24

Multiply each side by (-1).

x = 24

So, the measure of the angle is 24 degrees.

Problem 9 :

Two angles are supplementary. If the ratio of the measure of the smaller angle to that of the larger angle is 5:7. What is the measure of the smaller angle?

Solution :

Given : The ratio of the measure of the smaller angle to that of the larger angle is 5 : 7.

measure of the smaller angle = 5x

measure of the larger angle = 7x

Given : Two angles are supplementary.

5x + 7x = 180

12x = 180

Divide each side by 12.

x = 15

Measure of the smaller angle is

= 5x

= 5(15)

= 75°

So, the measure of the smaller angle is 75°.

Problem 10 :

The measure of supplement of an angle is equal to the twice the measure of the angle. What is the measure in degrees, of the compliment of the angle?

Solution :

Let x be the measure of the angle.

measure of supplement of the angle = 180° - x

Given : The measure of supplement of the angle is equal to the twice the measure of the angle.

(180° - x) is equal to 2x

180 - x = 2x

Add x to each side.

180 = 3x

Divide each side by 3.

60 = x

So, the measure of the angle is 60°.

Then, the measure of complement of the angle is

= 90 - 60

= 30°

So, the measure of compliment of  the angle is 30 degrees.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.