COMPLEMENTARY SUPPLEMENTARY VERTICAL ADJACENT AND CONGRUENT ANGLES

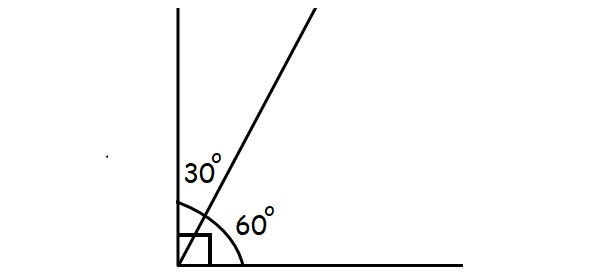
Complementary Angles

Two angles are said to be complementary to each other if sum of their measures is 90°.

For example, if ∠A = 52° and ∠B = 38°, then angles ∠A and ∠B are complementary to each other.

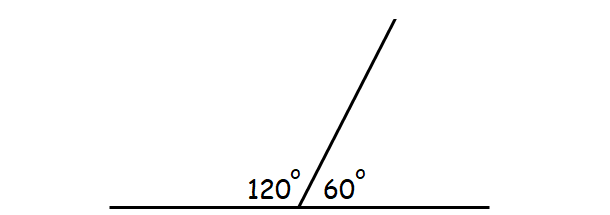
Supplementary Angles

Two angles are said to be supplementary to each other if sum of their measures is 180°.

For example, the angles whose measures are 112° and 68° are supplementary to each other.

Vertical Angles

The angles opposite each other when two lines cross. They are always equal.

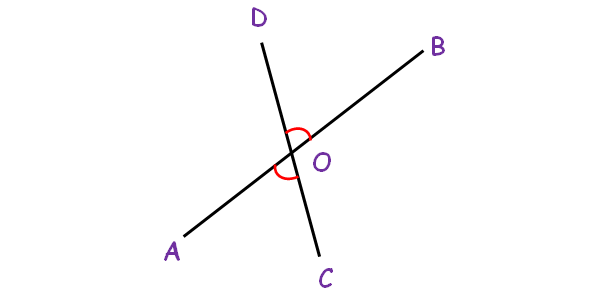
∠DOB = ∠AOC

∠DOA = ∠COB

Adjacent Angles 

Two angles are adjacent when they have common side and common vertex  and do not overlap.

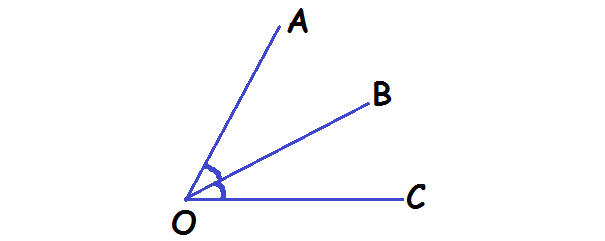
Angle AOC is adjacent to angle BOC

Because,

• they have a common side (line OB)
• they have a common vertex (point O)

Congruent Angles

Congruent Angles have the same angle

• They don't have to point in the same direction.
• They don't have to be on similar sized lines.
• Just the same angle.

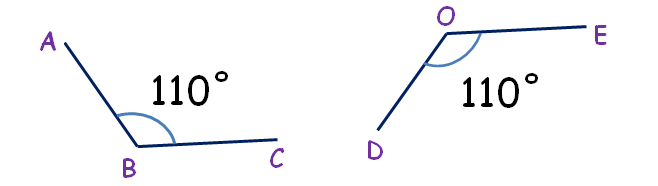
∠ABC = ∠DOE

Solved Problems 

Problem 1 :

Find the value of x in the diagram shown below.

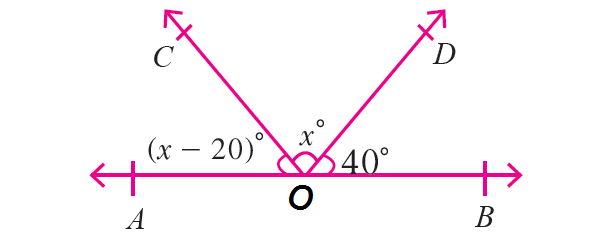
Solution :

Because all the three angle measures in the above diagram are on the same straight line AOB, they are supplementary.

(x - 20)° + x° + 40° = 180°

x - 20 + x + 40 = 180

2x + 20 = 180

Subtract 20 from each side.

2x = 160

Divide each side by 2.

x = 80

Problem 2 :

In the diagram shown below, if the lines AB and CD are parallel and  EF is transversal, find the value of x.

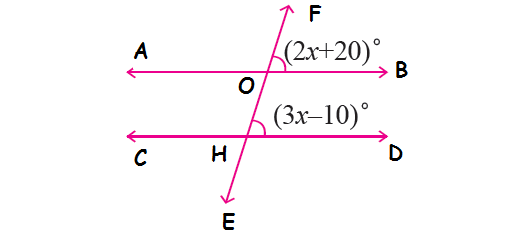
In the diagram shown above, because the lines AB and CD are parallel and EF is transversal, ∠FOB and ∠OHD are corresponding angles and they  are congruent.

∠FOB = ∠OHD

(2x + 20)° = (3x - 10)°

2x + 20 = 3x - 10

Subtract 2x from each side.

20 = x - 10

Add 10 to each side.

30 = x

Problem 3 :

In the diagram shown below, if the lines AB and CD are parallel and  EF is transversal, find the value of x.

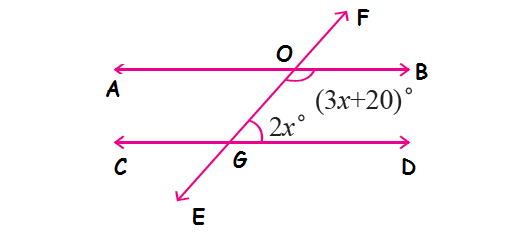
In the diagram shown above, because the lines AB and CD are parallel and EF is transversal, ∠BOG and ∠OGD are consecutive interior angles and they are supplementary.

∠BOG + ∠OGD = 180°

(3x + 20)° + 2x° = 180°

3x + 20 + 2x = 180

5x + 20 = 180

Subtract 20 from each side.

5x = 160

Divide each side by 5.

x = 32

Problem 4 :

Find the value of 'x' in the diagram shown below.

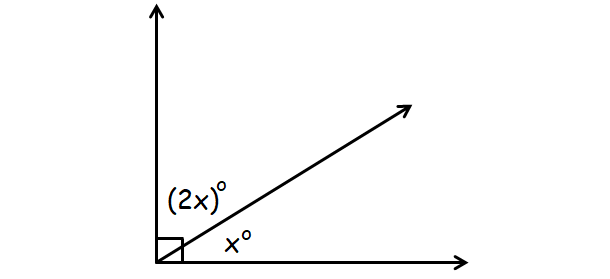
In the diagram shown below, it clear that the angle measures x° and (2x)° are complementary.

 (2x)° + x° = 90°

2x + x = 90

3x = 90

Divide each side by 3.

x = 30

Problem 5 :

Find the value of x in the diagram shown below.

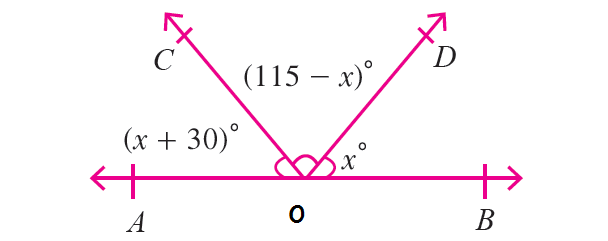
Solution :

Because all the three angle measures in the above diagram are on the same straight line AOB, they are supplementary.

(x + 30)° +  (115 - x)° + x° = 180°

x + 30 +  115 - x + x = 180

x + 145 = 180

Subtract 145 from each side.

x = 35

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.