COMPLETING THE SQUARE
Not every quadratic expression is a perfect square trinomial. Completing the square is the process of finding the constant to add to
x2 + bx
to create a perfect square trinomial.
Understand the Process of Completing the Square
The model below depicts the process of completing the square.
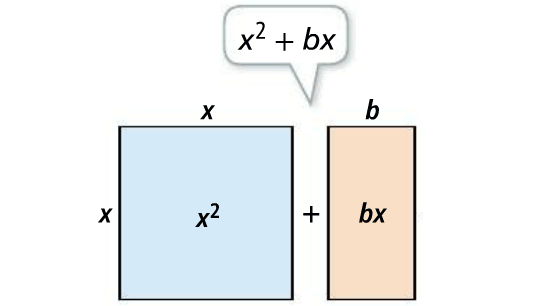

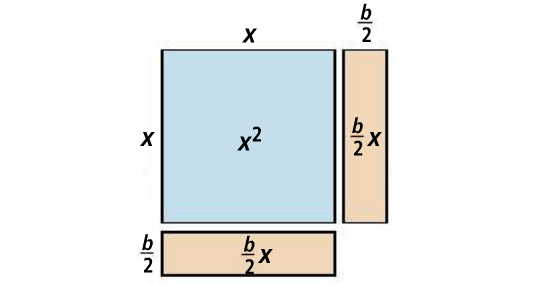

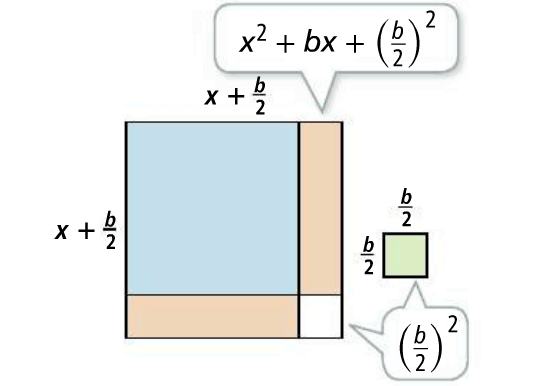
To create a perfect square trinomial, add (b/2)2 to the variable expression.
x2 + bx + (b/2)2 = (x + b/2)2
Example 1 :
Write x2 + 6x + 7 = 0 in the form (x + p)2 = q.
Solution :
Write the original equation.
x2 + 6x + 7 = 0
Isolate the variable expression.
x2 + 6x = -7 -----(1)
Determine the constant needed to complete the square.
Comparing x2 + bx and x2 + 6x, we get
b = 6
So,
(b/2)2 = (6/2)2 = 32 = 9
In (1), we have to add 9 to each side.
x2 + 6x + 9 = -7 + 9
Write the left side of the equation as a perfect square.
(x + 3)2 = 2
Hence, the equation x2 + 6x + 7 = 0 can be written as
(x + 3)2 = 2
Use Square Roots to Solve Quadratic Equations
Example 2 :
Solve the following quadratic equation using square root :
x2 + 12x + 36 = 49
Solution :
Write the original equation.
x2 + 12x + 36 = 49
Recognize that the quadratic equation is a perfect square trinomial.
x2 + 2(6)(x) + 62 = 49
Factor the perfect square trinomial.
(x + 6)2 = 49
Take the square root on each side of the equation.
√(x + 6)2 = ± √49
x + 6 = ± 7
x + 6 = -7 or x + 6 = 7
x = -13 or x = 1
Solving a Quadratic Equation by Completing the Square
Example 3 :
Solve the following quadratic equation by completing the square :
x2 - 8x - 9 = 0
Solution :
Write the original equation.
x2 - 8x - 9 = 0
Isolate the variable expression.
x2 - 8x = 9 -----(1)
Determine the constant needed to complete the square.
Comparing x2 + bx and x2 - 8x, we get
b = -8
So,
(b/2)2 = (-8/2)2 = (-4)2 = 16
In (1), we have to add 16 to each side.
x2 - 8x + 16 = 9 + 16
x2 - 8x + 16 = 25
Write the left side of the equation as a perfect square.
(x - 4)2 = 25
Take the square root on each side of the equation.
√(x - 4)2 = ± √25
x - 4 = ±5
x - 4 = -5 or x - 4 = 5
x = -1 or x = 9
Write a Quadratic Equation in Vertex Form
Example 4 :
Write the following quadratic equation in vertex form and graph it :
y = -x2 - 2x + 3
What is the maximum or minimum value of the graph of the equation ?
Solution :
Write the original equation.
y = -x2 - 2x + 3
Factor out the x2 coefficient, -1.
y = -1(x2 + 2x + 3)
= -1(x2 - 2 ⋅ x ⋅ 1 - 3)
= -1(x2 - 2 ⋅ x ⋅ 1 - 3)
= -1(x2 - 2 ⋅ x ⋅ 1 + 12 - 12 - 3)
= -[(x - 1)2 - 12 - 3]
= -[(x - 1)2 - 1 - 3]
= -[(x - 1)2 - 4]
= -(x - 1)2 + 4
Hence, the vertex form of the equation y = -x2 - 2x + 3 is
y = -(x - 1)2 + 4
Vertex :
The vertex of the parabola is (1, 4).
Graph :
In the given equation y = -x2 - 2x + 3, the sign of x2 is negative.
So, its graph is a parabola that opens downward.
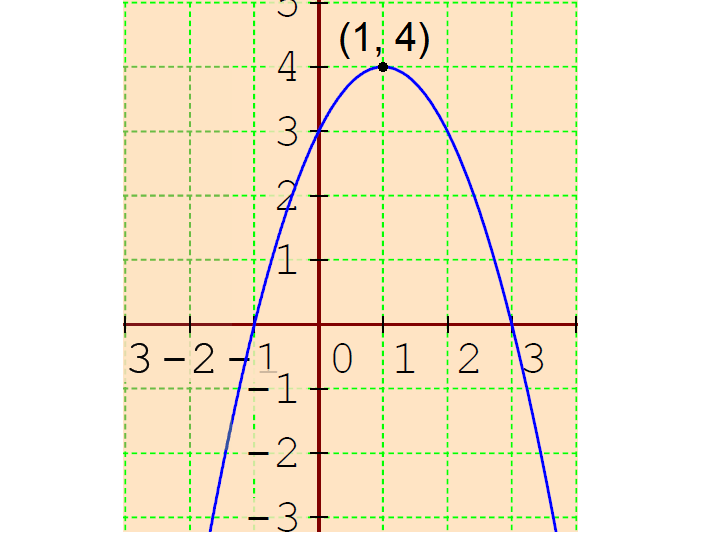
The graph of the given quadratic equation has a maximum of y = 4 at x = 1.
Complete the Square to Solve a Real-World Problem
Example 5 :
Alex plans to create rectangular shaped garden. He has 340 m of fencing available for the garden's perimeter and wants it to have an area of 6000 m2. What dimensions should Alex use ?
Solution :
Let x and y be the length and width of the garden respectively.
Given : Perimeter = 340.
So, we have
2x + 2y = 340
Divide each side by 2.
x + y = 170
Solve for y.
y = 170 - x
Alex wants the area to be 6000 m2.
Write this as an equation.
A = xy
6000 = x(170 - x)
6000 = 170x - x2
x2 - 170x = -6000 -----(1)
Determine the constant needed to complete the square.
Comparing x2 + bx and x2 - 170x, we get
b = -170
So,
(b/2)2 = (-170/2)2 = (-85)2 = 7225
In (1), we have to add 7225 to each side.
x2 - 170x + 7225 = -6000 + 7225
Write the left side of the equation as a perfect square.
(x - 85)2 = 1225
Take the square root on each side of the equation.
√(x - 85)2 = ±√1225
x - 85 = ±35
x - 85 = -35 or x - 85 = 35
x = 50 or x = 110
When x = 50,
y = 170 - 50
y = 120
When x = 110,
y = 170 - 110
y = 60
In each case, there is 340 m of fencing used.
Likewise, the area is 6000 m2.
Hence, Alex should make two sides of the garden 120 m long and the other two sides 50 m long.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 144)
Apr 14, 25 07:27 PM
Digital SAT Math Problems and Solutions (Part - 144) -
Quadratic Equation Problems with Solutions (Part - 1)
Apr 14, 25 11:33 AM
Quadratic Equation Problems with Solutions (Part - 1) -
Quadratic Equation Problems with Solutions (Part - 2)
Apr 14, 25 11:22 AM
Quadratic Equation Problems with Solutions (Part - 2)
