COMPLEX NUMBERS WITH INEQUALITY PROBLEMS

Question 1 :

If | z |= 3, show that 7 ≤ | z + 6 − 8i | ≤ 13.

Solution :

 | z + 6−8i | ≤ | [|z| + |6 − 8i|] |

 ≤ | 3 + √6² + (-8)²|

 ≤ |3 + √(36 + 64)|

 ≤ |3 + √100|

 ≤ |3 + 10|

 ≤ 13

 | z + 6−8i | ≥ |z| - |6 − 8i|

≥ |3 - √(36 + 64)|

≥ |3 - √100|

≥ |3 - 10|

≥  7

7  ≤ | z + 6−8i | ≤ 13

Question 2 :

If |z| = 1, show that 2 ≤ |z² -  3 | ≤ 4

Solution :

|z² -  3 | ≤ ||z²| + |- 3 | |

|z² -  3 | ≤ ||z|² + 3|

|z² -  3 | ≤ |1² + 3| 

|z² -  3 | ≤ 4

|z² -  3 | ≥  ||z²| - | 3||

|z² -  3 | ≥  |1 - 3|

|z² -  3 | ≥ 2

2 ≤ |z² -  3 | ≤ 4

Hence proved.

Question 3 :

If | z - (2/z) | = 2, show that the greatest and least value of | z | are √3 + 1 and √3 − 1 respectively

Solution :

|z - (2/z) | = 2

|(z² - 2)/z | = 2

Question 4 :

If z₁, z₂ and z₃ are three complex numbers such that |z₁| = 1, |z₂|  =  2, |z₃|  =  3 and |z₁ + z₂ + z₃|  =  1, show that |9 z₁ z₂ + 4 z₁ z₃ + z₂ z₃|  =  6

Solution :

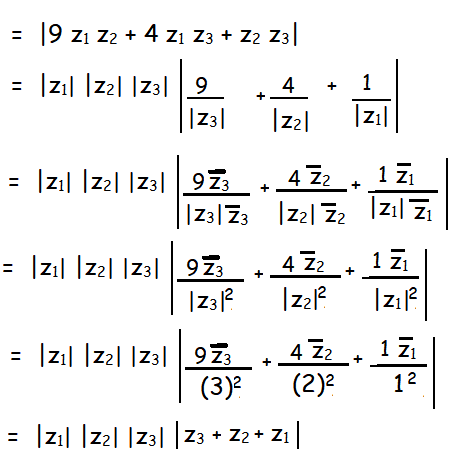
Now applying the given values, we get

  =  1(2)(3) (1)

  =  6

Hence proved.

Question 5 :

If the area of the triangle formed by the vertices z, iz , and z + iz is 50 square units, find the value of z .

Solution :

Length of three sides

z & iz  = √(z-0)² + (0-z)² = |z|√2  =  a

z & z + iz = √(z-z)² + (0-z)² = |z|  =  b 

z & z + iz = √(0-z)² + (z-z)² = |z|  =  c

The sides are |z|√2  , |z|  & |z|

s = (a + b + c)/2

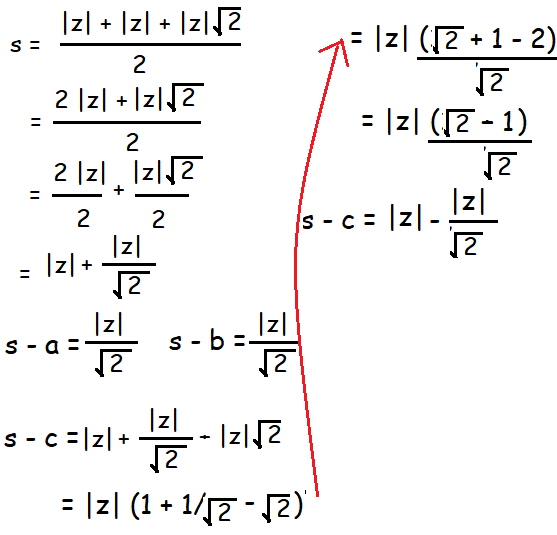
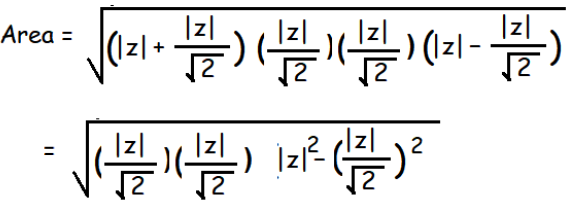
Area of triangle = 50 sq units

|z|²/2  =   50

|z|²  =  100

|z|  =  10

Hence the value of |z|  =  10.

Question 6 :

Show that the equation z³ + 2z bar = 0 has five solutions.

Solution :

z³ + 2z bar = 0

z = x + iy

(x + iy)³ + 2(x - iy)  =  0

x³ + 3x²(iy) + 3 x(iy)² + (iy)³ + 2x - i2y  =  0

x³ + i3x²y - 3 xy² - iy + 2x - i2y  =  0

(x³  - 3 xy² + 2x)  + i(3x²y - y - 2y)  =  0

(x³  - 3 xy² + 2x)  + i(3x²y - 3y)  =  0 + i0

By equating the real and imaginary parts, we get

x³  - 3 xy² + 2x  =  0 ----(1)

3x²y - 3y  =  0 ----(2) 

3y(x² - 1)  =  0

y  =  0, x  =  1, -1

By applying the two different values of x in (1), we get 2 different values of y.

Hence, it has 5 solutions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.