COMPOSITE FUNCTION

In general, suppose that f and g are two functions and that x is a number in the domain of g. By evaluating g at x, we get g(x). If g(x) is in the domain of f, then we may evaluate f at g(x) and obtain the result f[g(x)].

The correspondence from x to f[g(x)] is called a composite function f ∘ g.

Look at the picture carefully (shown below). Only those x's in the domain of g for which g(x) is in the domain of f can be in the domain of f ∘ g. The reason is that if g(x) is not in the domain of f then f[g(x)] is not defined. Because of this, the domain of f ∘ g is a subset of the domain of g; the range of f ∘ g is a subset of the range of f.

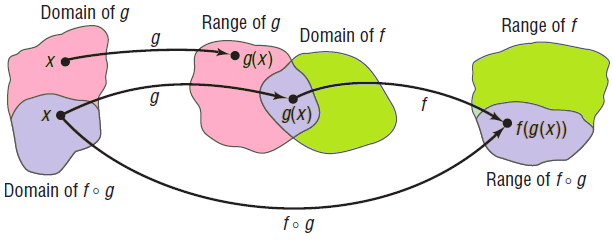
The picture shown below provides a second illustration of the definition. Here x is the input to the function g, yielding g(x). Then g(x) is the input to the function f, yielding f[g(x)]. Notice that the "inside" function g in f[g(x)] is done first.

Example 1 :

Let f(x) = 3x + 2 and g(x) = 5x. Find (f ∘ g) and (g ∘ f).

Solution :

f ∘ g :

f ∘ g = f[g(x)]

= f(5x)

= 3(5x) + 2

= 15x + 2

g ∘ f :

g ∘ f = g[f(x)]

= g(3x + 2)

= 5(3x + 2)

= 15x + 10

Example 2 :

Let f(x) = 2x² - 3 and g(x) = 4x. Find (f ∘ g) and (g ∘ f).

Solution :

f ∘ g :

f ∘ g = f[g(x)]

= f(4x)

= 2(4x)² - 3

= 2(4²x²) - 3

= 2(16x²) - 3

= 32x² - 3

g ∘ f :

g ∘ f = g[f(x)]

= g(2x² - 3)

= 4(2x² - 3)

= 8x² - 12

Example 3 :

Let f(x) = x + 3 and g(x) = x² - 9. Find (f ∘ g) and (g ∘ f).

Solution :

f ∘ g :

f ∘ g = f[g(x)]

= f(x² - 9)

= (x² - 9) + 3

= x² - 9 + 3

= x² - 6

g ∘ f :

g ∘ f = g[f(x)]

= g(x + 3)

= (x + 3)² - 9

= (x + 3)(x + 3) - 9

= x² + 3x + 3x + 9 - 9

= x² + 6x

Example 4 :

Let f(x) = log₁₀x and g(x) = 10^x. Find (f ∘ g) and (g ∘ f).

Solution :

f ∘ g :

f ∘ g = f[g(x)]

= f(10^x)

= log₁₀10^x

= xlog₁₀10

= x(1)

= x

g ∘ f :

g ∘ f = g[f(x)]

= g(log₁₀x)

= 10^log₁₀^x

= x

Here f ∘ g = g ∘ f = x.

So f(x) and g(x) are inverse to each other. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.