COMPOSITION OF FUNCTIONS WORKSHEET

Using the functions f and g given below, find f o g and g o f . Check whether  f o g = g o f .

Question 1 :

f(x) = x - 6, g(x) = x²               Solution

Question 2 :

 f(x) = 2/x, g(x) = 2x² - 1              Solution

Question 3 :

 f(x) = (x + 6)/3,  g(x) = 3 - x        Solution

Question 4 :

f(x) = 3 + x,  g(x) = x - 4          Solution

Question 5 :

f(x) = 4x² - 1, g(x) = 1 + x          Solution

Question 6 :

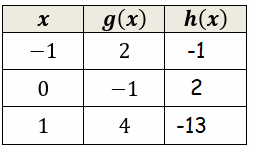
Let f(x) = 1 - 2x and h(x) = f(g(x)). Fill in the table.

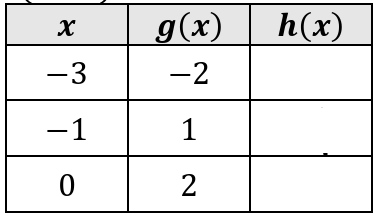
Solution

Question 7 :

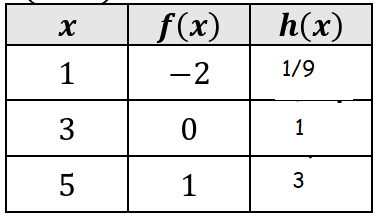
Let g(x) = 3^x and h(x) = g(f(x)). Fill in the table.

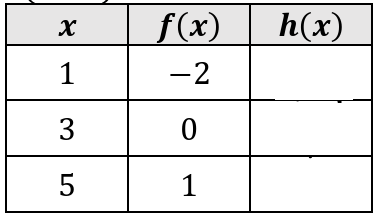
Solution

Question 8 :

Compare the quantity in column A with column B.

f(x) = 2x - 5 and g(x) = (1/2) (x + 5)

[A]The quantity in Column A is greater.

[B]The quantity in Column B is greater.

[C]The two quantities are equal.

[D]The relationship cannot be determined on the basis of the information supplied.

Solution

Question 9 :

Given 𝑓(𝑥)  = 5𝑥 - 2𝑏 while 𝑔(𝑥) = 4𝑏𝑥. If 𝑓[𝑔(1)] = 36, what is 𝑔(𝑓(1)) ?

Solution

Answer key

1)  f o g ≠ g o f

2)  f o g ≠ g o f

3)  f o g ≠ g o f

4)  f o g = g o f.

5)  f o g ≠ g o f.

6)  

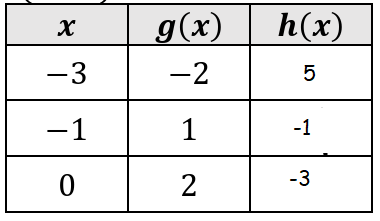
7)  

8)  [B]The quantity in Column B is greater is the correct answer.

9)  8

Question 1 :

f(x) = 3x + 2 and g(x) = 6x - k

Solution

Question 2 :

f(x) = 2x - k and g(x) = 4x + 5

Solution

Question 3 :

If f(x) = x² - 3x - 1 and g(x) = 1 - x, what is the value of (f o g)(-2)

A) -3    B) -1     C) 1     D) 3

Solution

Question 4 :

If f(x) = (1 - 5x)/2 and g(x) = 2 - x, what is the value of f(g(3)) ?

A) -7     B) -2    C) 2      D) 3

Solution

Question 5 :

If f = {(-4, 12)(-2, 4) (2, 0) (3, 3/2)} and g = { (-2, 5) (0, 1) (4, -7) (5, -9) }, what is the value of (g o f) (2)

A) -9     B) -7    C) 1      D) 5

Solution

Question 6 :

The function f satisfies f(-1) = 8 and f(1) = -2. A function g(2) satisfies g(2) = 5 and g(-1) = 1, what is the value of f(g(-1))

A) -9     B) -7    C) 1      D) 5

Solution

Question 7 :

g(x) = ax² + 24

for the function g defined above, a is constant  and g(4) = 8, what is the value of g(-4) ?

a)  8   b)  0   c)  -1    d)  -8

Solution

Question 8 :

If f(x) = √x + 2 and g(x) = -(x - 1)², which of the following is equivalent to g(f(a)) - 2f(a) ?

Solution

Question 9 :

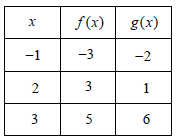
The table above gives values of f and g at selected values of x. What is the value of g(f(2)) ?

Solution

Question 1:

Let A, B, C ⊆ N and a function f : A -> B be defined by f(x) = 2x + 1 and g : B -> C be defined by g(x) = x² . Find the range of f o g and g o f.       Solution

Question 2 :

Let f(x) = x² - 1 . Find (i) f o f (ii) f o f o f      Solution

Question 3:

If f : R -> R and g : R -> R are defined by f(x) = x⁵ and g(x) = x⁴ then check if f, g are one-one and f o g is one-one?       Solution

Consider the functions f(x), g(x) and h(x) as given below. Find (f o g) o h and f o (g o h) in each case and also show that (f o g) o h = f o (g o h).

Question 1 :

f(x) = x - 1 , g(x) = 3x + 1 and h(x) = x²

Solution

Question 2 :

f(x) = x², g(x) = 2x and h(x) = x + 4

Solution

Question 3 :

f(x) = x - 4, g(x) = x² and h(x) = 3x - 5

Solution

Question 4 :

Given f(x) = -8x², g(x) = -3x + 9 and h(x) = √x, find [(f + g)o h] (x)

Solution

Question 5 :

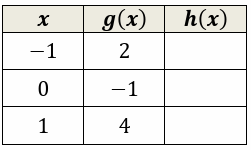
Let f(x) = 3 - x² and h(x) = f(g(x)). Fill the table.

Solution

Question 6 :

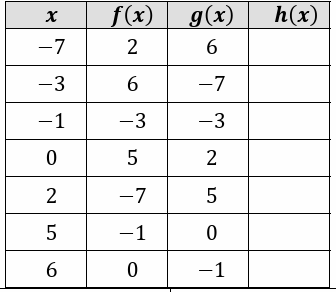
Fill in the following table, given that h(x) = f(g(x))

Solution

Question 7 :

Given 𝑓(𝑥)  = 5𝑥 - 2𝑏 while 𝑔(𝑥) = 4𝑏𝑥. If 𝑓(𝑔(1)) = 36, what is 𝑔(𝑓(1)) ?

Solution

Answer Key

1)  f o (g o h) = (f o g) o h

2)  f o (g o h) = (f o g) o h

3)  f o (g o h) = (f o g) o h

4)  -8x - 3√x - 9

5)  

6)  

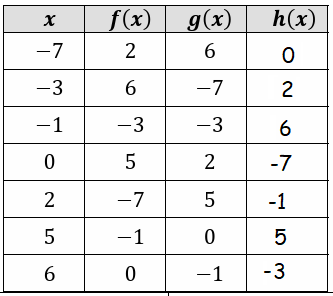
7)  b = 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.