COMPOSITION OF FUNCTIONS
When a car driver depresses the accelerator pedal, it controls the flow of fuel which in turn influences the speed of the car. Likewise, the composition of two functions is a kind of ‘chain reaction’, where the functions act upon one after another.
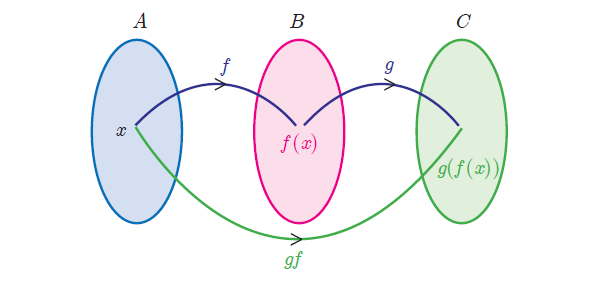
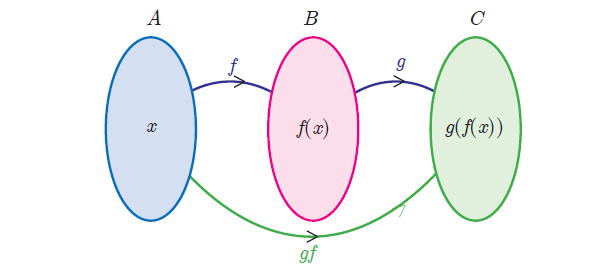
We can explain this further with the concept that a function is a ‘process’. If f and g are two functions then the composition g[f(x)] is formed in two steps.
(i) Feed an input (say x) to f ;
(ii) Feed the output f(x) to g to get g[f(x)] and call it
g o f
Illustration :
Consider the set A of all students, who appeared in class X of Board Examination in March 2020. Each student appearing in the Board Examination is assigned a roll number. In order to have confidentiality, the Board arranges to deface the roll number of each student and assigns a code number to each roll number.
Let A be the set of all students appearing for the board exam. B ⊆ ℕ be the set all roll numbers and C ⊆ ℕ be the set of all code numbers.
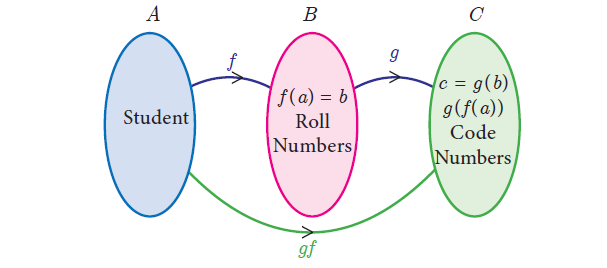
This gives rise to two functions f : A ---> B and g : B ---> C given by b = f(a) be the roll number assigned to student a, c = g(b) be the code number assigned to roll number b, where a ∈ A, b ∈ B and c ∈ C.
We can write c = g(b) = g[f(a)].
Thus, by the combination of these two functions, each student is eventually attached a code number. This idea leads to the following definition.
Definition :
Let f : A ----> B and g : B ----> C be two functions. Then the composition of f and g denoted by g o f is defined as the function g o f(x) = g[f(x)] for all x ∈ A.
Note :
Generally, f o g ≠ g o f for any two functions f and g. So, composition of functions is not commutative.
Problem 1 :
Find f o g and g o f when f(x) = 2x + 1 and g(x) = x2 - 2.
Solution :
f o g :
= f[g(x)]
= f[x2 - 2]
= 2(x2 - 2) + 1
= 2x2 - 4 + 1
= 2x2 - 3 ----(1)
g o f :
= g[f(x)]
= g[2x + 1]
= (2x + 1)2 - 2
= (2x)2 + 2(2x)(1) + 12 - 2
= 4x2 4x + 1 - 2
= 4x2 4x - 1 ----(2)
From (1) and (2), we see that f o g ≠ g o f.
Problem 2 :
Represent the following function as a composition of two functions.
h(x) = √(2x2 - 5x + 3)
Solution :
Let g(x) = 2x2 - 5x + 3 and f(x) = √x.
h(x) = √g(x)
= f[g(x)]
= f o g(x)
Problem 3 :
If f(x) = 3x - 2, g(x) = 2x + k and f o g = g o f, then find the value of k.
Solution :
f o g = g o f
f[g(x)] = g[f(x)]
f[2x + k] = g[3x - 2]
3(2x + k) - 2 = 2(3x - 2) + k
6x + 3k - 2 = 6x - 4 + k
Subtract 6x from each side.
3k - 2 = -4 + k
Subtract k from each side.
2k - 2 = -4
Add 2 to each side.
2k = -2
Divide each side by 2.
k = -1
Problem 4 :
Find k if f o f(k) = 5 where f(k) = 2k - 1 .
Solution :
f o f(k) = 5
f[f(k)] = 5
f[2k - 1] = 5
2(2k - 1) - 1 = 5
4k - 2 - 1 = 5
4k - 3 = 5
Add 3 to each side.
4k = 8
Divide each side by 2.
k = 2
Composition of Three Functions
Let A, B, C, D be four sets and let f : A--->B , g : B--->C and h : C--->D be three functions.
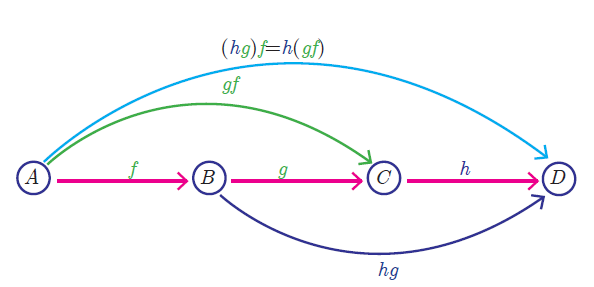
Using composite functions f o g and g o h, we get two new functions like (f o g) o h and f o (g o h).
We observed that the composition of functions is not commutative. The natural question is about the associativity of the operation.
Composition of three functions is always associative. That is,
f o (g o h) = (f o g) o h
Problem 5 :
f(x) = 2x + 3 , g(x) = 1 - 2x and h(x) = 3x . Prove that
f o (g o h) = (f o g) o h
Solution :
f o (g o h) :
|
g o h = g[h(x)] = g[3x] = 1 - 2(3x) = 1 - 6x |
f o (g o h) = f[1 - 6x] = 2(1 - 6x) + 3 = 2 - 12x + 3 = 5 - 12x ----(1) |
(f o g) o h :
|
f o g = f[g(x)] = f[1 - 2x] = 2(1 - 2x) + 3 = 5 - 4x |
(f o g) o h = (f o g)[h(x)] = (f o g)(3x) = 5 - 4(3x) = 5 - 12x ----(2) |
From (1) and (2),
f o (g o h) = (f o g) o h
Problem 6 :
If f(x) = 3x + 1, g(x) = x + 3 and gff(x) = fgg(x), find x.
Solution :
gff(x) = fgg(x)
g{f[f(x)]} = f{g[g(x)]}
g{f[3x + 1]} = f{g[x + 3]}
g{3(3x + 1) + 1} = f{(x + 3) + 3}
g{9x + 3 + 1} = f{x + 6}
g{9x + 4} = f{x + 6}
(9x + 4) + 3 = 3(x + 6) + 1
9x + 4 + 3 = 3x + 18 + 1
9x + 7 = 3x + 19
Subtract 3x and 7 from each side.
6x = 12
Divide each side by 6.
x = 2
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Permutation Problems with Solutions
May 08, 25 12:28 PM
Permutation Problems with Solutions -
Digital SAT Math Problems and Solutions (Part - 159)
May 08, 25 01:39 AM
Digital SAT Math Problems and Solutions (Part - 159) -
Digital SAT Math Problems and Solutions (Part - 158)
May 06, 25 11:00 AM
Digital SAT Math Problems and Solutions (Part - 158)