COMPOUND FRACTIONS

A compound fraction is a fraction in which the numerator, the denominator, or both, are themselves fractional expressions.

Examples : 

(1/a)/(b/2), (x + 1/y)/(y + 1/x)

Simplifying a Compound Fraction : Method I

Step 1 : 

Simplify the numerator and the denominator of the complex fraction so that each is a single fraction.

Step 2 : 

To divide the fraction in numerator by the fraction in denominator, invert the divisor and multiply.

Step 3 : 

Simplify if possible.

Example 1 : 

(2x/27y²)/(6x²/9)

Solution : 

=  (2x/27y²)/(6x²/9)

The numerator of the compound fraction is already a single fraction, and so is the denominator.

Invert the the fraction in denominator and multiply.

=  (2x/27y²) ⋅ (9/6x²)

=  (2x ⋅ 9) / (6x² ⋅ 27y²)

Cancel common factors. 

=  1 / (3x ⋅ 3y²)

=  1/9xy²

Example 2 : 

(x/y + 1)/(1 - y/x)

Solution : 

=  (x/y + 1)/(1 - y/x)

We combine the terms in the numerator into a single fraction and do the same in the denominator. Then we invert and multiply.

=  [(x + y)/y]/[(x - y)/x]

Invert the the fraction in denominator and multiply.

=  [(x + y)/y)] ⋅ [x/(x - y)]

=  [x(x + y)] / [y(x - y)]

Simplifying a Compound Fraction : Method II

Step 1 : 

Find the least common denominator (LCD) of the fractions in both numerator and denominator of the compound fraction.

Step 2 : 

Multiply the numerator and the denominator of the compound fraction by the LCD found in step 1. 

Step 3 : 

Simplify if possible.

Example 3 : 

[5x/(x + 2)]/[10/(x - 2)]

Solution : 

=  [5x/(x + 2)]/[10/(x - 2)]

The least common denominator of the fractions in both numerator and denominator is (x + 2)(x - 2). 

Multiply numerator and denominator by the LCD.

=  [5x/(x + 2)](x + 2)(x - 2) / [10/(x - 2)](x + 2)(x - 2)

Simplify.

=  [5x(x - 2)]/[10(x + 2)]

=  x(x - 2)/2(x + 2)

Example 4 :

[x/y² + 1/y] / [y/x² + 1/x]

Solution : 

=  [x/y² + 1/y] / [y/x² + 1/x]

The least common denominator of the fractions in both numerator and denominator is x²y². 

Multiply numerator and denominator by the LCD.

=  [x/y² + 1/y](x²y²) / [y/x² + 1/x](x²y²)

Use the distributive property.

=  [x/y² ⋅ x²y² + 1/y ⋅ x²y²] / [y/x² ⋅ x²y² + 1/x ⋅ x²y²]

Simplify. 

=  [x³ + x²y]/[y³ + xy²]

Factor. 

=  [x²(x + y)]/[y²(y + x)]

=  x²/y²

Example 5 :

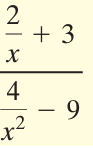
Solution :

Simplifying the numerator :

= (2/x) + 3

= (2 + 3x)/x

Simplifying the denominator :

= (4/x²) - 9

= (4 - 9x²) / x²

= (2² - (3x)²) / x²

= (2 + 3x)(2 - 3x) / x²

Dividing the numerator by denominator, we get

= [(2 + 3x)/x] ÷ [(2 + 3x)(2 - 3x) / x²]

= [(2 + 3x)/x] x [ x²/ (2 + 3x)(2 - 3x)]

= (2 - 3x)/x

Example 6 :

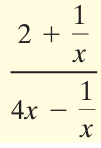
Solution :

Simplifying the numerator :

= 2 + (1/x)

= (2x + 1)/x

Simplifying the denominator :

= 4x - (1/x)

= (4x² - 1)/x

= ((2x)² - 1²)/x

= (2x + 1)(2x - 1)/x

Dividing the numerator by denominator, we get

= [(2x + 1)/x] ÷ [(2x + 1)(2x - 1)/x]

= [(2x + 1)/x] x [x/(2x + 1)(2x - 1)]

= 1/(2x - 1)

Example 7 :

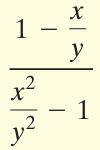
Solution :

Simplifying the numerator :

= 2 + (1/x)

= (2x + 1)/x

Simplifying the denominator :

= 4x - (1/x)

= (4x² - 1)/x

= ((2x)² - 1²)/x

= (2x + 1)(2x - 1)/x

Dividing the numerator by denominator, we get

= [(2x + 1)/x] ÷ [(2x + 1)(2x - 1)/x]

= [(2x + 1)/x] x [x/(2x + 1)(2x - 1)]

= 1/(2x - 1)

Example 8 :

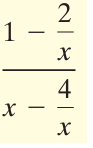
Solution :

Simplifying the numerator :

= 1 - (2/x)

= (x - 2)/x

Simplifying the denominator :

= x - (4/x)

= (x² - 4)/x

= (x² - 2²)/x

= (x + 2)(x - 2)/x

Dividing the numerator by denominator, we get

= [(x - 2)/x] ÷ [(x + 2)(x - 2)/x]

= [(x - 2)/x] x [x/(x + 2)(x - 2)]

= (x + 2)

Example 9 :

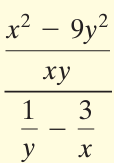
Solution :

Simplifying the numerator :

= (x² - 9y²)/xy

= (x² - (3y)²)/xy

= (x + 3y)(x - 3y)/xy

Simplifying the denominator :

= 1/y - (3/x)

= (x - 3y)/xy

Dividing the numerator by denominator, we get

= [(x + 3y)(x - 3y)/xy] ÷ [(x - 3y)/xy]

= [(x + 3y)(x - 3y)/xy] x [xy/(x - 3y)]

= (x + 3y)

Example 10 :

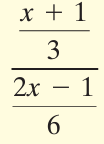
Solution :

Simplifying the numerator :

= (x + 1)/3

Simplifying the denominator :

= (2x - 1)/6

Dividing the numerator by denominator, we get

= [ (x + 1)/3] ÷ [ (2x - 1)/6]

= [(x + 1)/3] x [6/(2x - 1)]

= 2(x + 1)/(2x - 1)

Example 11 :

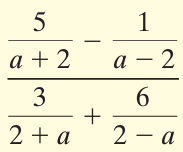
Solution :

Simplifying the numerator :

= 5/(a + 2) - 1/(a - 2)

= [5(a - 2) - 1(a + 2)]/(a + 2)(a - 2)

= [5a - 10 - a - 2]/(a + 2)(a - 2)

= (a - 12)/(a + 2)(a - 2)

Simplifying the denominator :

= 3/(2 + a) + 6/(2 - a)

= 3/(a + 2) - 6/(a - 2)

3(a - 2) - 6(a + 2) / (a + 2)(a - 2)

= (3a - 6 - 6a - 12) / (a + 2)(a - 2)

= (-3a - 18) / (a + 2)(a - 2)

= -3(a + 6) / (a + 2)(a - 2)

Dividing the numerator by denominator, we get

= (a - 12)/(a + 2)(a - 2) ÷ [-3(a + 6) / (a + 2)(a - 2) ]

= (a - 12)/(a + 2)(a - 2) x [-(a + 2)(a - 2)/3(a + 6) ]

= -(a - 12)/3(a + 6)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.