COMPOUND INEQUALITIES AND OR

Compound Inequalities with "And"

A compound inequality containing and is true only if both inequalities are true. Thus, the graph of a compound inequality containing and is the intersection of the graphs of the two inequalities.

In other words, the solution must be a solution of both inequalities.

That is, we have to shade the portion that we find in both graphs. If the particular region is not in one of the graphs, we should not shade the region.

Compound Inequalities with "Or"

Another type of compound inequality contains the word or. A compound inequality containing or is true if one or more of the inequalities is true. The graph of a compound inequality containing or is the of the graphs of the two inequalities.

In other words, the solution of the compound inequality is a solution of either inequality, not necessarily both. The union can be found by graphing each inequality.

Example 1 :

Solve each compound inequality. Then graph the solution set.

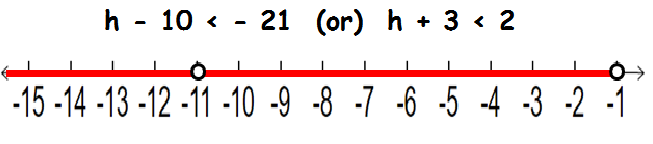
h - 10 < - 21  (or)  h + 3 < 2

Solution : 

h - 10 < - 21  (or)  h + 3 < 2

Now let us graph for the first inequality

h < -11

We have to shade the portion, which is lesser than -11. Since it is less than sign, we have to use the unfilled circle 

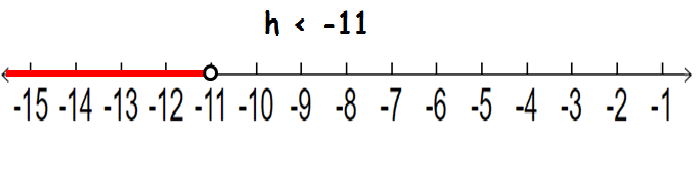
Now let us graph for the second inequality

h < -1

We have to shade the portion, which is lesser than -1. Since it is less than sign, we have to use the unfilled circle 

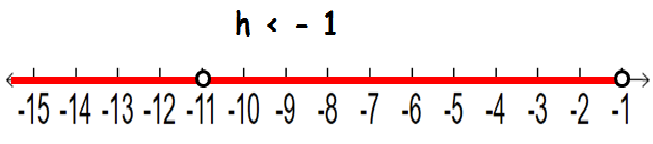
By combining the above two graphs, we get

Example 2 :

Solve the compound inequality. Then graph the solution set

k + 2 > 12 and k + 2 ≤ 18

Solution :

By graphing the inequality k > 10, we get the graph given below.

By graphing the inequality ≤ 16, we get the graph given below.

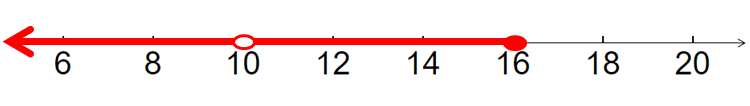
By combining the above two graphs, we get the common region between 10 and 16.

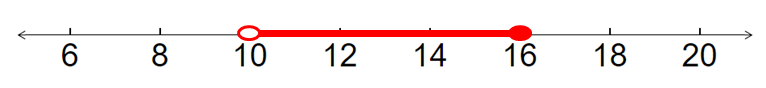
Write an sentence as an inequality. Graph the inequality.

Example 3 :

A number p is less than 6 and greater than 2.

Solution :

• P should be less than 6, then p < 6
• p should be greater than 4, then p > 4

Using the operation and in the middle,

p < 6 and p > 4

Since we have only less than sign (<) and greater than sign (>), we have to use transparent circle near 6 and 4.

Example 4 :

A number n is less than or equal to -7 or greater than 12

Solution :

• n should be less than or equal to -7, then p ≤ -7
• n should be greater than 12, then p > 12

Using the operation or in the middle,

p ≤ -7 or p > 12

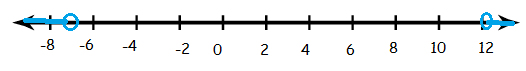
Example 5 :

Write a compound inequality for each solution set shown below.

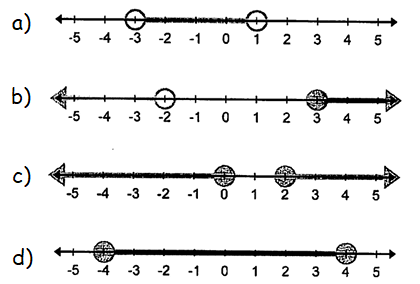
Solution : 

Graph a :

We observe that the shaded part is in between -3 and 1.

• At -3, we have transparent circle. All values which are greater than -3
• At 1 also, we have transparent circle. All values which are lesser than 1.

Combining these two, writing it as inequality we get

-3 < x < 1

Graph b :

• At -2, we have transparent circle. All values which are lesser than -2
• At 1 also, we have solid circle. All values which are greater than or equal to 3

Combining these two, writing it as inequality we get

x < -2 or x ≥ 3

Writing using interval notation, we get

(-∞, -2) U [3, ∞)

Graph c :

• At 0 and 2, we have transparent circle.
• All values which are lesser than or equal to 0 and all the values which are greater than or equal to 2.

Combining these two, writing it as inequality we get

x ≤ 0 or x ≥ 2

Writing using interval notation, we get

(-∞, 0] U [2, ∞)

Graph d :

We observe that the shaded part is in between -4 and 4.

• At -4, we have solid circle. All values which are greater than -4
• At 4 also, we have solid circle. All values which are lesser than 4.

Combining these two, writing it as inequality we get

-4 ≤ x ≤ 4

Example 6 :

Create a compound inequality for the following word problems

a)  Nine less than a number is no more than 8 and is no less than 3.

b) The sum of four times a number and eight is between 0 and 12.

Solution :

a)

• Nine less than a number, then x - 9
• It is no more than 8 and no less than 3. So, in between 3 and 8.

3 ≤ x - 9 ≤ 8

b)

We consider the required number be x.

• The sum of four times a number and 8. Then 4x + 8
• Lies between 0 and 12.

0 < 4x + 8 < 12

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.