CONDITION FOR LINES TO BE PERPENDICULAR

(i) Condition for lines to be perpendicular in terms of their slopes.

Let m₁ and m₂ be the slopes of two lines.

If, the two lines are perpendicular, then the product of their slopes is equal to - 1

That is, 

m₁ x m₂  =  -1

(ii)  Condition for lines to be perpendicular in terms of their general form of equations.

Let us consider the general form of equation of a straight line ax + by + c  =  0.  

If the two lines are perpendicular, then their general form of equations will differ as shown in the figure below.

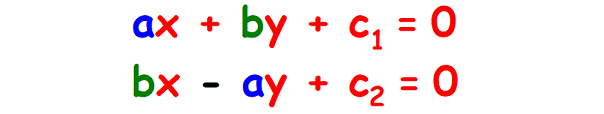
(iii)  Condition for lines to be perpendicular in terms of their slope-intercept form of equations.

Let us consider the slope intercept form of equation of a straight line  y  =  mx + b.  

If the two lines are perpendicular, then their slope-intercept form equations will differ as given in the figure below

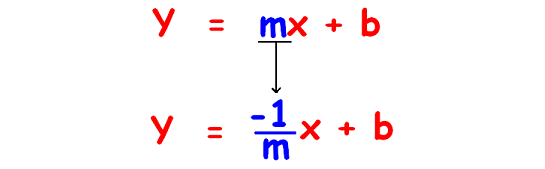
Practice Problems

Problem 1 :

The slopes of the two lines are 7 and (3k + 2). If the two lines are perpendicular, find the value of 'k'.

Solution :

If the given two lines are perpendicular, then the product of the slopes is equal to  -1.

7(3k + 2)  =  - 1

Use distributive property. 

21k + 14  =  -1

Subtract 14 from each side. 

21k  =  -15

Divide each side by 21. 

k  =  -15/21

k  =  -5/7

Problem 2 :

The equations of the two perpendicular lines are

3x + 2y - 8  =  0

(5k+3) - 3y + 1  =  0

Find the value of 'k'.

Solution :

If the two lines are perpendicular, then the coefficient 'y' term in the first line is equal to the coefficient of 'x' term in the second line. 

Then,

5k + 3  =  2

Subtract 3 from each side. 

5k  =  -1

Divide each side by 5.

k  =  -1/5

Problem 3 :

Find the equation  of a straight line is passing through (2, 3) and perpendicular to the line 2x - y + 7  =  0. 

Solution :

Required line is perpendicular to 2x - y + 7  =  0.

Then, the equation of the required line is

x  + 2y + k  =  0 -----(1)

The required line is passing through (2, 3).

Substitute x  =  2 and y  = 3  in  (1).

(1)-----> 2 + 2(3) + k  =  0

2 + 6 + k  =  0

8 + k  =  0

Subtract 8 from each side. 

k  =  -8

Problem 4 :

Verify, whether the following two lines  re perpendicular.

3x - 2y - 7  =  0

y  =  -(2x/3) + 4

Solution :

In the equations of the given two lines, the equation of the second line is not in general form. 

Let us write the equation of the second line in general form. 

y  =  - (2x/3) + 4

Multiply each side by 3.

3y  =  - 2x + 12

2x + 3y - 12  =  0

Compare the equations of two lines, 

3x - 2y - 7 = 0

2x + 3y - 12  =  0

When we look at the general form of equations of the above two lines, we get the following points. 

(i) The sign of 'y' terms are different.

(ii) The coefficient of 'x' term in the first equation is the coefficient of "y" term in the second equation. 

(iii) The coefficient of 'y' term in the first equation is the coefficient of 'x' term in the second equation. 

(iv)  The above equations differ in constant terms. 

Considering the above points, it is clear that the given two lines are perpendicular. 

Problem 5 :

Verify, whether the following two lines are perpendicular.

5x + 7y - 1  =  0

14x - 10y + 5  =  0

Solution :

In the equation of the second line 14x - 10y + 5 = 0, the coefficients of 'x' and 'y' have the common divisor 2. 

Divide the second equation by 2.

(14x/2) - (10y/2) + (5/2)  =  (0/2)

7x - 5y + 2.5  =  0

Compare the equations of two lines, 

5x + 7y - 1  =  0

7x - 5y + 2.5  =  0

When we look at the general form of equations of the above two lines, we get the following points. 

(i) The sign of y- terms are different.

(ii) The coefficient of 'x' term in the first equation is the coefficient of "y" term in the second equation. 

(iii) The coefficient of 'y' term in the first equation is the coefficient of 'x' term in the second equation. 

(iv)  The above equations differ in constant terms. 

Considering the above points, it is clear that the given two lines are perpendicular.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.