CONDITIONAL  TRIGONOMETRIC IDENTITIES

Example 1 :

If A + B + C = π/2, prove that 

sin2A + sin2B + sin2C = 4cosAcosBcosC

Solution :

sin2A + sin2B + sin2C :

= 2sin(A + B)cos(A - B) + sin2C

= 2sin(90 - C)cos(A - B) + 2sinCcosC

= 2cosCcos(A - B) + 2sinCcosC

= 2cosC[cos(A - B) + sinC]

= 2cosC[cos(A - B) + sin(90 - (A + B)]

= 2cosC[cos(A - B) + cos(A + B)]

= 2cosC[2cosAcos(-B)]

= 2cosC[2cosAcosB]

= 4cosAcosBcosC

Example 2 :

If A + B + C = π/2, prove that 

cos2A + cos2B + cos2C = 1 + 4sinAsinBcosC

Solution :

cos2A + cos2B + cos2C :

Use the identity of (cosC + cosD) for cos2A + cos2B.

= 2cos(A + B)cos(A - B) + cos2C

= 2cos(90 - C)cos(A - B) + 1 - 2sin²C

= 2sinCcos(A - B) + 1 - 2sin²C

= 1 + 2sinC[cos(A - B) - sinC]

= 1 + 2sinC[cos(A - B) - sin(90 - (A + B)]

= 1 + 2sinC[cos(A - B) - cos(A + B)]

= 1 + 2sinC[-2sinAsin(-B)]

= 1 + 2sinC[2sinAsinB]

= 1 + 4sinAsinBsinC

Example 3 :

If triangle ABC is a right triangle and ∠A = π/2, then prove that

(i) cos²B + cos²C = 1

(ii) sin²B + sin²C = 1

(iii) cosB - cosC = -1 + 2√2cos(B/2)sin(C/2)

Solution :

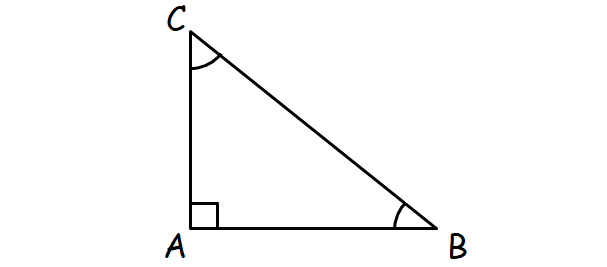
(i) cos² B + cos² C = 1 :

In the right triangle ABC above, 

cosθ = Adjacent side/Hypotenuse

cosB = AB/BC

cosC = AC/BC

cos²B + cos²C  =  (AB/BC)² + (AC/BC)² 

  =  (AB² + AC²)/BC²

  =  BC²/BC²

  =  1

(ii) sin² B + sin² C = 1 :

In the right triangle ABC above, 

sinθ = Opposite side/Hypotenuse

sinB = AC/BC

sinC = AB/BC

 sin²B + sin²C = (AC/BC)² + (AB/BC)²

= AC²/BC² + (AB²/BC²)

= (AC² + AB²)/BC²

= BC²/BC²

= 1

(iii) cosB − cosC = -1 + 2 √2 cos B/2 sin C/2 :

cosB - cosC = 2cos²B - 1 - cosC

= -1 + 2cos²B - cosC ----(1)

In the triangle ABC above, 

A + B + C = π

It is given that A = π/2. Then, 

B + C = π/2

C = π/2 - B

Substitute C = π/2 - B in (1).

= -1 + 2cos²(B/2) - cos(π/2 - B)

= -1 + 2cos²(B/2) - sinB

= -1 + 2cos²(B/2) - 2sin(B/2)cos(B/2)

= -1 + 2cos(B/2)(cos(B/2) - sin(B/2))

B = π/2 - C ----> B/2 = π/4 - C/2

= -1 + 2cos(B/2)[cos(π/4 -  C/2) - sin(π/4 - C/2)]

= -1 + 2cos(B/2)[cos(π/4 -  C/2) - cos(π/2 - (π/4 - C/2))]

= -1 + 2cos(B/2)[cos(π/4 -  C/2) - cos(π/4 + C/2)]

= -1 + 2cos(B/2)[-2sin(π/4)sin(-C/2)]

= -1 + 2cos(B/2)[2(1/√2)sin(C/2)]

= -1 + 2√2cos(B/2)sin(C/2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.