CONGRUENCE AND TRIANGLES WORKSHEET

Problem 1 :

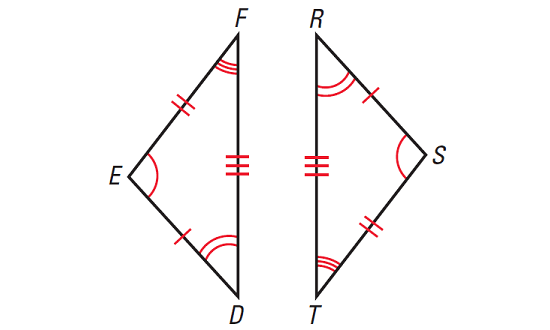
The congruent triangles represent the triangles in the diagram given below. Write a congruence statement. Identify all pairs of congruent corresponding parts.

Problem 2 :

In the diagram given below, NPLM ≅ EFGH.

(i) Find the value of x.

(ii) Find the value of y.

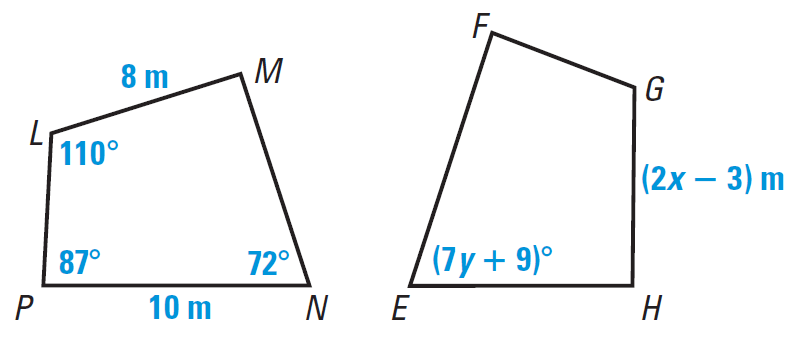
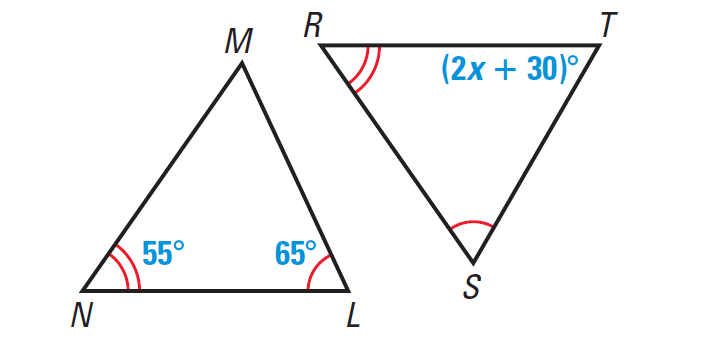
Problem 3 :

Find the value of x in the diagram given below.

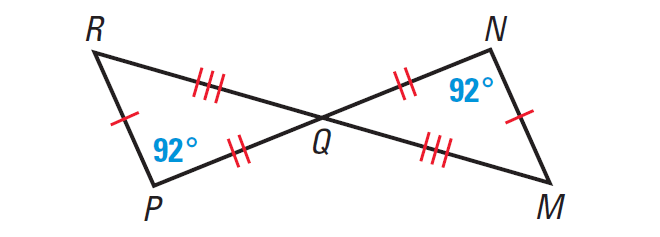
Problem 4 :

Decide whether the triangles are congruent. Justify your reasoning.

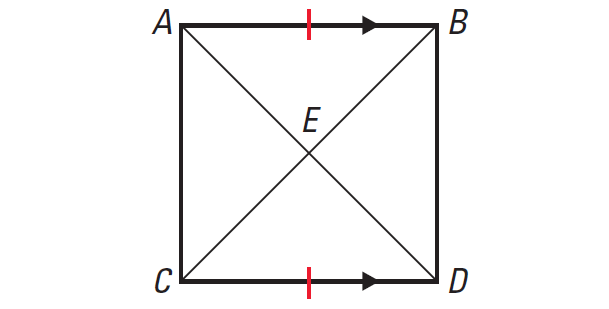
Problem 5 :

In the diagram given below, prove that ΔAEB ≅ ΔDEC.

1. Answer :

The diagram indicates that ΔDEF ≅  ΔRST.

The congruent angles and sides are as follows.

Angles :

∠D ≅ ∠R, ∠E ≅ ∠S and ∠F ≅ ∠T

Sides :

DE ≅ RS, EF ≅ ST and FD ≅ TR

2. Answer :

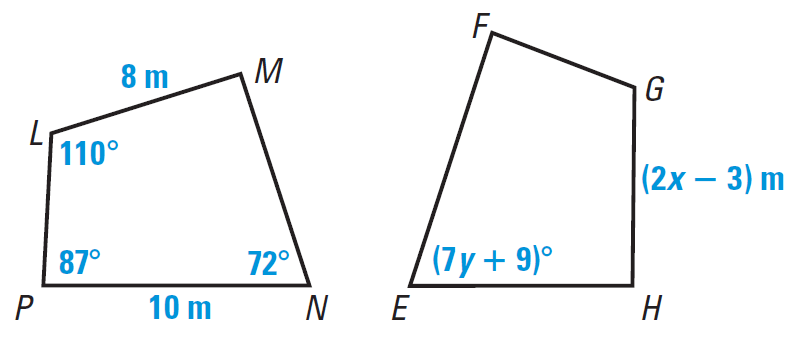
Part (i) :

We know that LM ≅ GH.

So, we have

LM = GH

8 = 2x - 3

Add to 3 to both sides.

11 = 2x

Divide both sides by 2.

5.5 = x

Part (ii) :

We know that ∠N ≅ ∠E.

So, we have

m∠N = m∠E

72° = (7y + 9)°

72 = 7y + 9

Subtract 9 from both sides.

63 = 7y

Divide both sides by 7.

9 = y

3. Answer :

In the diagram given above, ∠N ≅ ∠R and ∠L ≅ ∠S. From the Third angles theorem, we know that ∠M ≅ ∠T. So, m∠M = m∠T.

From the triangle sum theorem, we have

m∠L + m∠M + m∠N = 180°

65° + 55° + m∠M = 180°

120° + m∠M = 180°

Subtract 120° from both sides.

m∠M = 60° 

By Third angles theorem, we have

m∠M = m∠T

Substitute 60° for m∠M and (2x + 30)° for m∠M.

60° = (2x + 30)°

60 = 2x + 30

Subtract 30 from both sides.

30 = 2x

Divide both sides by 2.

15 = x

4. Answer :

From the diagram, we are given that all three pairs of corresponding sides are congruent.

RP ≅ MN, PQ ≅ NQ and QR ≅ QM

Because ∠P and ∠N have the same measure, ∠P ≅ ∠N.

By the Vertical Angles Theorem, we know that

ΔPQR ≅ ΔNQM

By the Third Angles Theorem,

∠R ≅ ∠M

So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent. By the definition of congruent angles,

ΔPQR ≅ ΔNQM

5. Answer :

Given :

AB || DC and AB ≅ DC

E is the midpoint of BC and AD

To prove :

ΔAEB ≅ ΔDEC

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.