CONGRUENCE MODULO

Two integers a and b are congruence modulo n if they differ by an integer multiple of n. That b - a = kn for some integer k.

This can also be written as a ≡ b (mod n). Here the number n is called modulus.

In other words, a ≡ b(mod n) means a -b is divisible by n

For example, 61 ≡ 5 (mod 7) because 61 – 5 = 56 is divisible by 7.

1. When a positive integer is divided by n, then the possible remainders are 0, 1, 2, . . . , n - 1.

2. Thus, when we work with modulo n, we replace all the numbers by their remainders upon division by n, given by 0, 1 ,2, 3, ..., n - 1.

Example 1 :

Find 8 (mod 4).

Solution :

With a modulus of 4 (since the possible remainders are 0, 1, 2, 3) we make a diagram like a clock with numbers 0, 1, 2, 3.

We start at 0 and go through 8 numbers in a clockwise sequence 1, 2, 3, 0, 1, 2, 3, 0.

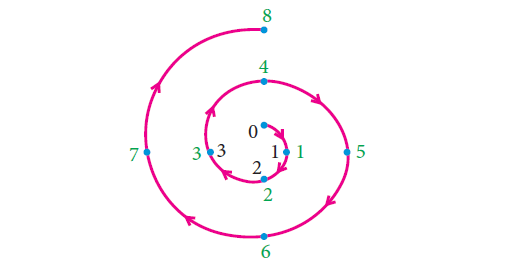
After doing so cyclically, we end at 0.

Therefore, 8 ≡ 0 (mod 4).

Example 2 :

Find -5 (mod 3).

Solution :

With a modulus of 3 (since the possible remainders are 0, 1, 2, 3) we make a diagram like a clock with numbers 0, 1, 2.

We start at 0 and go through 5 numbers in anti-clockwise sequence 2, 1, 0, 2, 1.

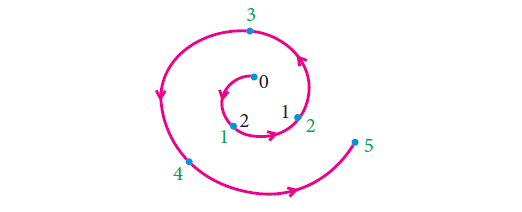
After doing so cyclically, we end at 0.

Therefore, -5 ≡ 1 (mod 3).

Connecting Euclid’s Division lemma and Modular Arithmetic

Let m and n be integers, where m is positive. Then by Euclid’s division lemma, we can write

n = mq + r

where 0 ≤ r < m and q is an integer.

Instead of writing n = mq + r, we can use the congruence notation in the following way.

We say that n is congruent to r modulo m, if n = mq + r for some integer q.

n = mq + r

n - r = mq

n - r ≡ 0 (mod m)

n ≡ r (mod m)

Thus the equation n = mq + r through Euclid’s Division lemma can also be written as n ≡ r (mod m).

Note :

Two integers a and b are congruent modulo m, written as

a ≡ b (mod m),

if they leave the same remainder when divided by m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.