CONGRUENT CHORDS AND ARCS

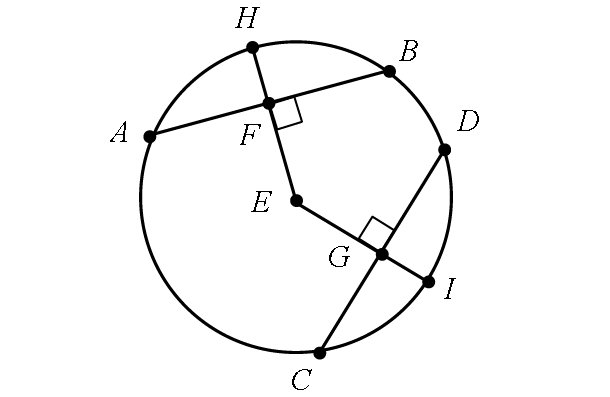
Two chords are congruent if and only if : 

(i) Their corresponding arcs are congruent. 

AB  =  CD  <----->  m∠arc AB  =  m∠arc CD

(ii) They are equidistant from the center. 

AB  =  CD  <----->  EF  =  EG

If a diameter or radius is perpendicular to a chord, then it bisects the chord and its arc. 

In the diagram shown above, 

EH ⊥ AB -----> AF  =  FB  and m∠arc AH  =  m∠arc HB

Example 1 :

Find x. 

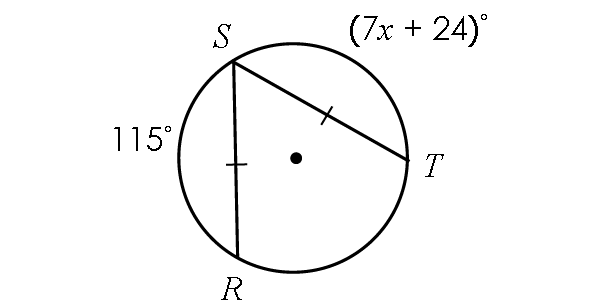
Solution :

In the diagram above, the two chords ST and RS are congruent. 

Then, 

ST  =  RS

7x + 24  =  115

Subtract 24 from each side. 

7x  =  91

Divide each side by 7. 

x  =  13

Example 2 :

Find x. 

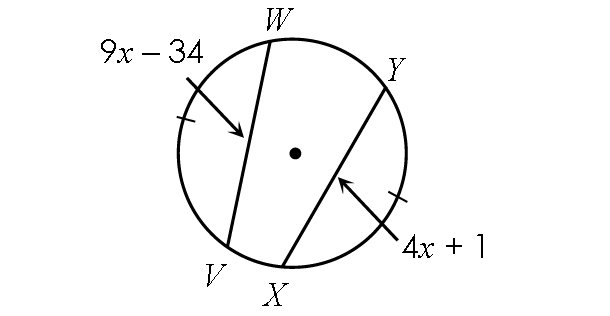
Solution :

In the diagram above, the two chords VW and XY are congruent. 

Then, 

WV  =  XY

9x - 34  =  4x + 1

Subtract 4x from each side. 

5x - 34  =  1

Add 34 to each side.

5x  =  35

Divide each side by 5. 

x  =  7

Example 3 :

Find x. 

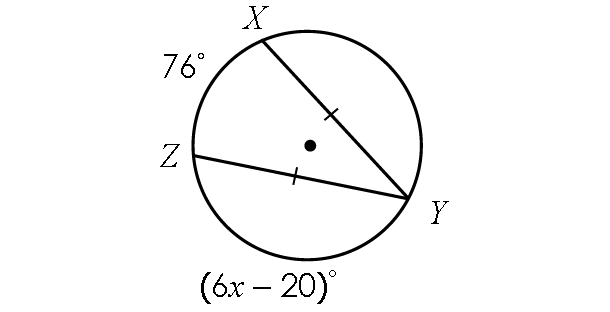
Solution :

In the diagram above,

m∠arc YZ  =  (6x - 20)°

And also, the two chords YZ and XY are congruent.

Then,

m∠arc XY  =  m∠arc YZ

m∠arc XY  =  (6x - 20)°

In the circle above, 

m∠arc XY + m∠arc YZ + m∠arc ZX  =  360°

(6x - 20)° + (6x - 20)° + 76°  =  360°

6x - 20 + 6x - 20 + 76  =  360

Combine the like terms. 

12x + 36  =  360

Subtract 36 from each side. 

12x  =  324

Divide each side by 12.

x  =  27

Example 4 :

If MP  =  5x - 34, PN  =  2x - 4, find MP. 

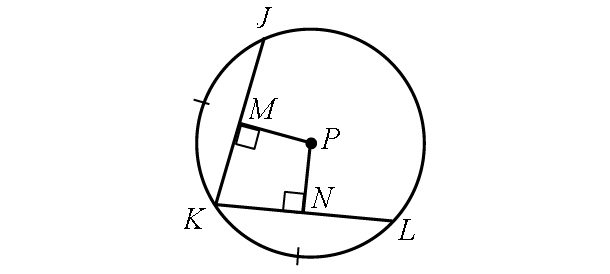
Solution :

In the diagram above,

m∠arc JK  =  m∠arc KL

Then, the two chords JK and KL are congruent.

Because the two chords JK and KL are congruent, they are equidistant from the center. 

Then, 

MP  =  PN

5x - 34  =  2x - 4

Subtract 2x from each side. 

3x - 34  =  -4

Add 34 to each side. 

3x  =  30

Divide each side by 3. 

x  =  10

Find MP : 

MP  =  5x - 34

Substitute x  =  10. 

MP  =  5(10) - 34

MP  =  50 - 34

MP  =  16

Example 5 :

If QM  =  6x - 11 and MR  =  2x + 9, find MN. 

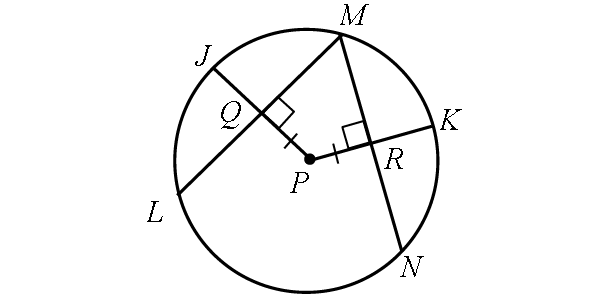
Solution :

In the diagram above, the two chords LM and MN are equidistant from the center.

Then, the two chords LM and MN are congruent.

The radii JP and KP are perpendicular to the chords LM and MN respectively.

Then, they bisect the chords. 

Because the chords LM and MN are congruent and they are bisected by the radii, 

QM  =  MR

6x - 11  =  2x + 9

Subtract 2x from each side. 

4x - 11  =  9

Add 11 to each side.

4x  =  20

Divide each side by 4. 

x  =  5

Find MN : 

MN  =  2(MR)

MN  =  2(2x + 9)

MN  =  4x + 18

Substitute x  =  5. 

MN  =  4(5) + 18

MN  =  20 + 18

MN  =  38

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.