CONGRUENT TRIANGLES ON THE COORDINATE PLANE

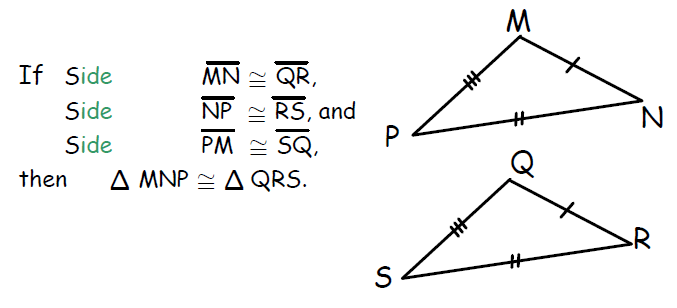
By SSS triangle congruence postulate, if three sides of one triangle are congruent to three sides of another second triangle, then the two triangles are congruent.

Given two triangles on a coordinate plane, we can check whether they are congruent by using the  distance formula to find the lengths of their sides. If three pairs of sides are congruent, then the triangles are congruent by the above postulate. 

The diagram given below illustrates this. 

Problem 1 :

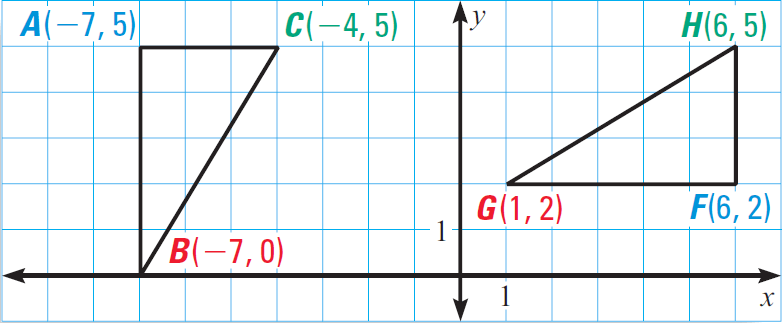
In the diagram given below, prove that ΔABC  ≅  ΔFGH. 

Solution :

Because AB = 5 in triangle ABC and FG = 5 in triangle FGH, 

AB  ≅  FG.

Because AC = 3 in triangle ABC and FH = 3 in triangle FGH, 

AC  ≅  FH.

Use the distance formula to find the lengths of BC and GH. 

Length of BC :

BC  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  B(-7, 0) and (x₂, y₂)  =  C(-4, 5)

BC  =  √[(-4 + 7)² + (5 - 0)²]

BC  =  √[3² + 5²]

BC  =  √[9 + 25]

BC  =  √34

Length of GH :

GH  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  G(1, 2) and (x₂, y₂)  =  H(6, 5)

GH  =  √[(6 - 1)² + (5 - 2)²]

GH  =  √[5² + 3²]

GH  =  √[25 + 9]

GH  =  √34

Conclusion :

Because BC = √34 and GH = √34,

BC  ≅  GH

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔABC  ≅  ΔFGH

Problem 2 :

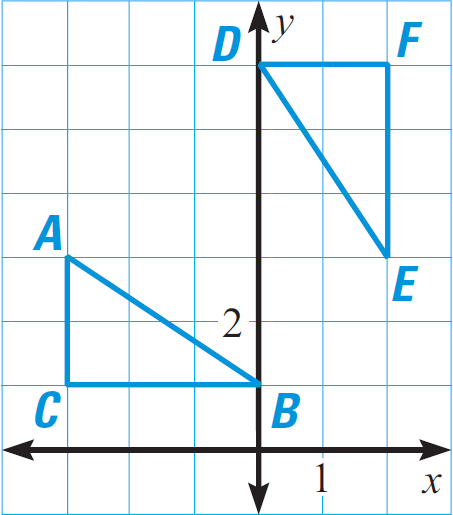
In the diagram given below, prove that ΔABC  ≅  ΔDEF. 

Solution :

From the diagram given above, we have

A(-3, 3), B(0, 1), C(-3, 1), D(0, 6), E(2, 3), F(2, 6)

Because AC = 2 in triangle ABC and DF = 2 in triangle DEF, 

AC  ≅  DF.

Because BC = 3 in triangle ABC and EF = 3 in triangle DEF, 

BC  ≅  EF.

Use the distance formula to find the lengths of BC and GH. 

Length of AB :

AB  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  A(-3, 3) and (x₂, y₂)  =  B(0, 1)

AB  =  √[(0 + 3)² + (1 - 3)²]

AB  =  √[3² + (-2)²]

AB  =  √[9 + 4]

AB  =  √13

Length of DE :

DE  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  D(0, 6) and (x₂, y₂)  =  E(2, 3)

DE  =  √[(2 - 0)² + (3 - 6)²]

DE  =  √[2² + (-3)²]

DE  =  √[4 + 9]

DE  =  √13

Conclusion :

Because AB = √13 and DE = √13,

AB  ≅  DE

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔABC  ≅  ΔDEF 

Problem 3 : 

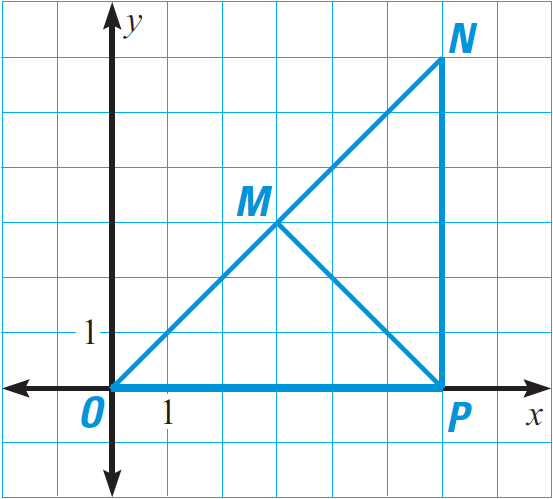
In the diagram given below, prove that ΔOPM  ≅  ΔMNP. 

Solution :

PM is the common side for both the triangles OPM and MNP. 

Because OP = 6 in triangle OPM and PN = 6 in triangle MNP, 

OP  ≅  PN.

Use the distance formula to find the lengths of OM and MN. 

Length of OM : 

OM  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  O(0, 0) and (x₂, y₂)  =  M(3, 3)

OM  =  √[(3 - 0)² + (3 - 0)²]

OM  =  √[3² + 3²]

OM  =  √[9 + 9]

OM  =  √18

Length of MN : 

MN  =   √[(x₂ - x₁)² + (y₂ - y₁)²]

Here (x₁, y₁)  =  M(3, 3) and (x₂, y₂)  =  N(6, 6)

MN  =  √[(6 - 3)² + (6 - 3)²]

MN  =  √[3² + 3²]

MN  =  √[9 + 9]

MN  =  √18

Conclusion :

Because  OM = √18 and MN = √18,

OM  ≅  MN

All the three pairs of corresponding sides are congruent. By SSS congruence postulate, 

ΔOPM  ≅  ΔMNP

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.