CONJUGATE OF A COMPLEX NUMBER

The conjugate of the complex number x + iy is defined as the complex number x - iy.

If z represents a complex number, then the complex conjugate of z is denoted by z̄. To get the conjugate of the complex number z, simply change the sign of i in z. For instance, 2 - 3i is the conjugate of 2 + 3i.

The product of a complex number with its conjugate is a real number. For instance,

(i) (a + ib)(a - ib) :

= a² - (ib)²

= a² - i²b²

= a² - (-1)b²

= a² + b²

(i) (3 + 4i)(3 - 4i) :

= 3² - (4i)²

= 9 - 4²i²

= 9 - 4(-1)

= 9 + 4

= 13

Geometrically, the conjugate of of the complex number z is obtained by reflecting z on the real axis.

Geometrical Representation of Conjugate of a Complex Number

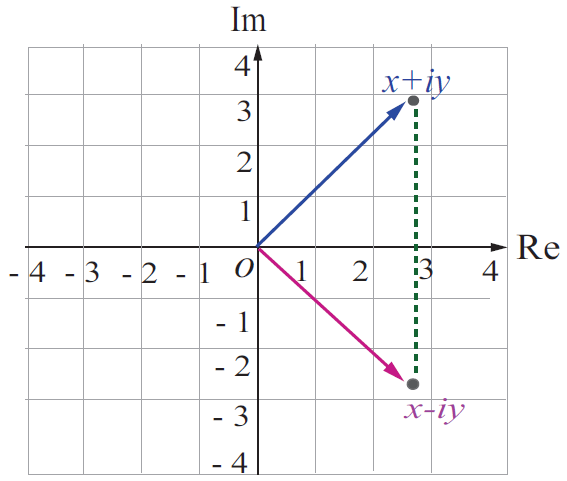
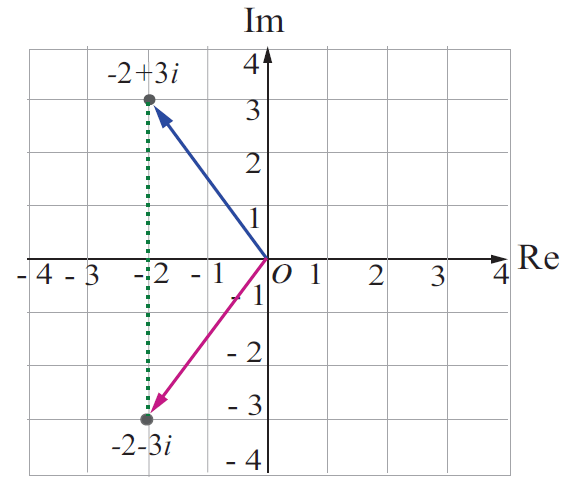
Note :

Two complex numbers x + iy and x - iy are conjugates to each other. The conjugate is useful in division of complex numbers. The complex number can be replaced with a real number in the denominator by multiplying the numerator and denominator by the conjugate of the denominator. This process is similar to rationalising the denominator to remove surds.

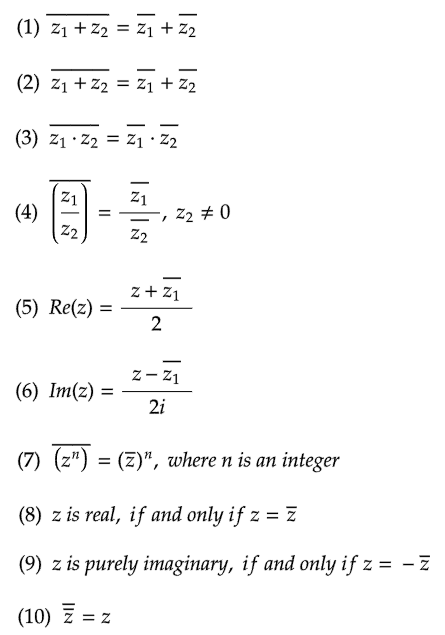
Solve Problems

Problem 1 :

Write the complex number given below in x + iy form, hence find its real and imaginary parts.

Solution :

To express the given complex number in the rectangular form x + iy, multiply the numerator and denominator by the conjugate of the denominator to eliminate i in the denominator.

The complex number above is in the form x + iy.

Problem 2 :

Simplify the following expression into rectangular form.

Solution :

We consider

and

Therefore,

Problem 3 :

In the expression given below, find the complex number z in the rectangular form.

Solution :

2(z + 3) = (z - 5i)(1 + 4i)

2z + 6 = z + 4zi - 5i - 20i²

2z + 6 = z + 4zi - 5i - 20(-1)

2z + 6 = z + 4zi - 5i + 20

2z - z - 4zi = -5i + 20 - 6

z - 4zi = -5i + 14

z(1 - 4i) = 14 - 5i

Problem 4 :

Solution :

Problem 5 :

Find z^-1, if z = (2 + 3i)(1 - i).

Solution :

z = (2 + 3i)(1 - i)

= 2 - 2i + 3i - 3i²

= 2 + i - 3(-1)

= 2 + i + 3

= 5 + i

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.