CONE

Cone is the solid that is generated by rotating a line segment which is passing through a fixed point and making a constant angle with a fixed line.

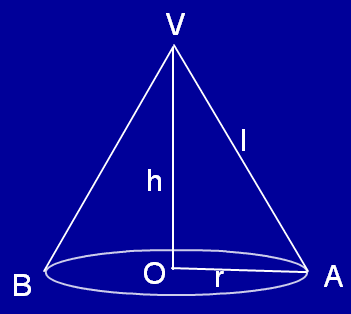
In the above figure here , VO is a fixed line and VA is a rotating line which is making constant angle with VO. The point A would describe a circle with center O such that the line segment VO is perpendicular to the base.

VO is the height h and OA is the base radius r VA is the slant height l.

It is very clear VAO is right angled triangle and the right angle is at at O.

Since VAO is the right angled triangle by Pythagorean theorem

we have l² = h² + r²

If we know the value of the other two measurements.

For example, if we have the height h, and the radius r , we can easily determine the value of the slant height l.

Example 1 :

If the height and radius of a right circular conoid are 4cm and 3cm respectively, find the slant height.

Solution :

Let us plug the known values in to the equation.

l²  =  h² + r²

l²  =  4² + 3²

l²  =  16 + 9

l²  =  25

So, slant height is is 5 cm.

Example 2 :

A heap of paddy is in the form of a conoid whose diameter is 4.2 m and height is 2.8 m. If the heap is to be covered exactly by a canvas to protect it from rain, then find the area of the canvas needed.

Solution :

Diameter of heap of paddy = 4.2 m

r  =  4.2/2

=  2.1 m

height of paddy (h) = 2.8 m

l²  =  r²+h²

l  =  √(2.1)²+(2.8)²

l  =  √(4.41+7.84)

l  =  √12.25

l  =  3.5 cm

Curved surface area of heap of paddy = Π r l

=  (22/7) ⋅ (2.1) ⋅ (3.5)

=  22 ⋅ (2.1) ⋅(0.5)

=  23.1 cm²

Curved surface area of paddy is 23.1 cm².

Example 3 :

Consider the semi-circular piece of paper shown.

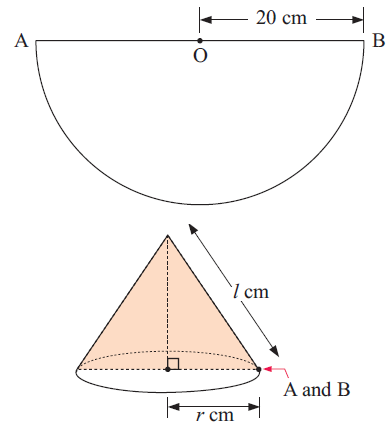
When sides [OA] and [OB] are put together, we form a cone.

a) Find the value of l.

b) Find the circumference of the base of the cone.

c) Use b to find r.

d) Find the area of the base of the cone.

e) Find the area of the curved surface of the cone.

f) Find the total surface area of the cone.

Solution :

(a)  When we rotate the semicircular shape into cone, the radius will become slant height.

Radius of semicircle  =  slant height  =  10 cm

(b)  Circumference of base  =  2πr

=  2 x π x 20

=  40 π

(c)   Circumference of base of cone  =  πr

=  10 π

Radius of base of cone  =  10 cm.

d) Find the area of the base of the cone.

=  πr²

=  π(10)²

=  100π

e) Find the area of the curved surface of the cone.

Curved surface area  =  πrl

=  π(10)(10)

=  100π

f) Find the total surface area of the cone.

=  πr(l+r)

=  π(10)(10+10)

=  200π

Example 4 :

The surface area of the cone is 100𝛑 square meters. What is the slant height ℓ of the cone?

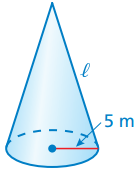
Solution :

Surface area of cone = πrl

r = 5 m

πrl = 100π

5l = 100

l = 100/5

l = 20 m

So, the required slant height is 20 m.

Example 5 :

You design a party hat. You attach a piece of elastic along a diameter.

(a) How long is the elastic?

(b) How much paper do you need to make the hat?

Solution :

a) To find the length of the elastic, we have to find the length of the diameter.

Circumference of circle = 2πr

2πr = 22

2 x 3.14 x r = 22

r = 22/(2 x 3.14)

r = 3.5

2r = 2(3.5)

= 7 inches

So, the length of the elastic is 7 inches.

b)  Surface area of cone = πrl

= 3.14 x 3.5 x 5

= 54.95 square inches.

Example 6 :

A paper cup shaped like a cone has a diameter of 6 centimeters and a slant height of 7.5 centimeters. How much paper is needed to make the cup

Solution :

Diameter = 6 inches

radius = 3 inches

Slant height = 7.5 inches

Material required = πrl

= 3.14 x 3 x 7.5

= 70.65 square inches.

Example 7 :

How much material is needed to make the Nón Lá Vietnamese leaf hat

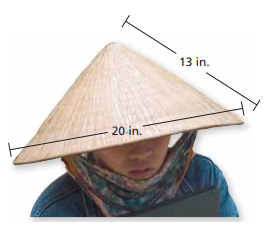
Solution :

Diameter = 20 inches

radius = 10 inches

Slant height = 13 inches

Material required = πrl

= 3.14 x 10 x 13

= 408.2 square inches.

Example 8 :

The volume of a right circular cone is 9856 cm³, if the diameter of the base is 28 cm, find its height.

Solution :

Volume of cone = 1/3 πr² h

diameter = 28 cm

radius = 14 cm

1/3 πr² h = 9856 cm³

(1/3) x 3.14 x 14² x h = 9856 cm³

h = 9856 x 3 x (1/3.14 x 196)

h = 48.04 cm

Example 9 :

If the volume and height of a cone are 500 cm³ and 15 cm, then find the radius of base of the cone. .

Solution :

Volume of cone = 1/3 πr² h

radius = 15 cm

1/3 πr² h = 500 cm³

(1/3) x 3.14 x r² x 15 = 500 cm³

r² = 500 x 3 x (1/3.14 x 15)

r² = 31.84 cm

r = 5.64 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.