CONSTANT OF PROPORTIONALITY

The value of the constant of proportionality is depending on the type of proportion we have between the two quantities. 

There are two types of proportion: 

1. Direct proportion

2. Inverse proportion

Direct Proportion

If y is directly proportional to x, then we have

where k is the constant of proportionality.

Inverse Proportion

If y is inversely proportional to x, then we have

where k is the constant of proportionality.

Identifying Proportional Relationships

If two different quantities are given, how to check whether the relationship between them is proportional ? 

We have to get ratio of the two quantities for all the given values. 

If all the ratios are equal, then the relationship is proportional. 

If all the ratios are not equal, then the relationship is not proportional. 

Identifying Proportional Relationships - Examples

Example 1 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

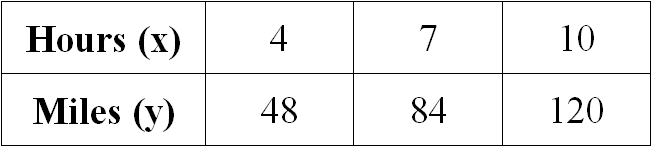
Solution : 

Let us get the ratio of x and y for all the given values. 

4 / 48  =  1 / 12

7 / 84  =  1 / 12

10 / 120  =  1 / 12

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.   

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion. 

Then, we have 

y  =  kx 

Substitute 4 for x and 48 for y. 

48  =  k(4)

12  =  k

So, the constant of proportionality is 12.

Example 2 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

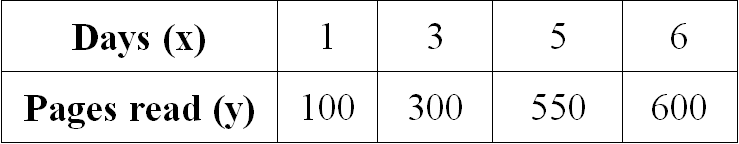
Solution : 

Let us get the ratio of x and y for all the given values. 

1 / 100  =  1 / 100

3 / 300  =  1 / 100

5 / 550  =  1 / 110

6 / 600  =  1 / 100

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

So, the relationship given in the table is not proportional. 

Example 3 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

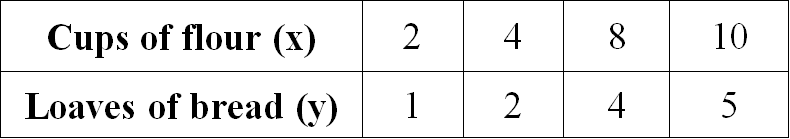
Solution : 

Find the ratio of x and y for all the given values. 

2 / 1  =  2

4 / 2  =  2

8 / 4  =  2

10 / 5  =  2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore, the relationship given in the table is proportional.   

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion. 

Then, we have 

y  =  kx 

Substitute 2 for x and 1 for y.

1  =  k(2)

1 / 2  =  k

So, the constant of proportionality is 1/2.

Example 4 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

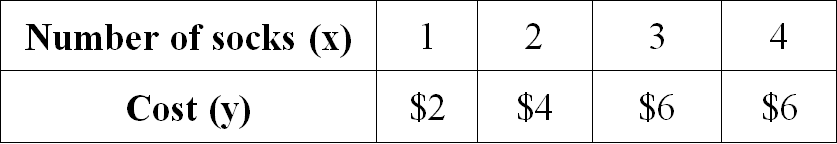
Solution : 

Find the ratio of x and y for all the given values. 

1 / 2  =  1 / 2

2 / 4  =  1 / 2

3 / 6  =  1 / 2

4 / 6  =  2 / 3

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

So, the relationship given in the table is not proportional.

Example 5 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

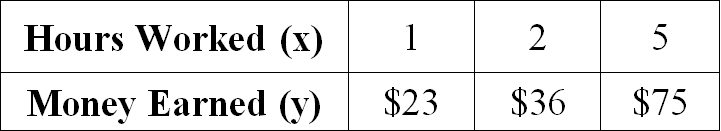
Solution : 

Find the ratio of x and y for all the given values. 

1 / 23  =  1 / 23

2 / 36  =  1 / 18

5 / 75  =  1 / 15

When we take ratio of x and y for all the given values, we don't get equal value for all the ratios.

So, the relationship given in the table is not proportional. 

Example 6 :

Examine the given table and determine if the relationship is proportional. If yes, determine the constant of proportionality. 

Solution : 

Find the ratio of x and y for all the given values. 

2 / 4  =  1 / 2

4 / 8  =  1 / 2

6 / 12  =  1 / 2

8 / 16  =  1 / 2

When we take ratio of x and y for all the given values, we get equal value for all the ratios.

Therefore the relationship given in the table is proportional.   

When we look at the above table when x gets increased, y also gets increased, so it is direct proportion. 

Then, we have 

y  =  kx

Substitute 2 for x and 4 for y. 

4  =  k(2)

2  =  k

So, the constant of proportionality is 2.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

WORD PROBLEMS

HCF and LCM  word problems

Word problems on simple equations 

Word problems on linear equations 

Word problems on quadratic equations

Algebra word problems

Word problems on trains

Area and perimeter word problems

Word problems on direct variation and inverse variation 

Word problems on unit price

Word problems on unit rate 

Word problems on comparing rates

Converting customary units word problems 

Converting metric units word problems

Word problems on simple interest

Word problems on compound interest

Word problems on types of angles 

Complementary and supplementary angles word problems

Double facts word problems

Trigonometry word problems

Percentage word problems 

Profit and loss word problems 

Markup and markdown word problems 

Decimal word problems

Word problems on fractions

Word problems on mixed fractions

One step equation word problems

Linear inequalities word problems

Ratio and proportion word problems

Time and work word problems

Word problems on sets and Venn diagrams

Word problems on ages

Pythagorean theorem word problems

Percent of a number word problems

Word problems on constant speed

Word problems on average speed 

Word problems on sum of the angles of a triangle is 180 degree

OTHER TOPICS 

Profit and loss shortcuts

Percentage shortcuts

Times table shortcuts

Time, speed and distance shortcuts

Ratio and proportion shortcuts

Domain and range of rational functions

Domain and range of rational functions with holes

Graphing rational functions

Graphing rational functions with holes

Converting repeating decimals in to fractions

Decimal representation of rational numbers

Finding square root using long division

L.C.M method to solve time and work problems

Translating the word problems in to algebraic expressions

Remainder when 2 power 256 is divided by 17

Remainder when 17 power 23 is divided by 16

Sum of all three digit numbers divisible by 6

Sum of all three digit numbers divisible by 7

Sum of all three digit numbers divisible by 8

Sum of all three digit numbers formed using 1, 3, 4

Sum of all three four digit numbers formed with non zero digits

Sum of all three four digit numbers formed using 0, 1, 2, 3

Sum of all three four digit numbers formed using 1, 2, 5, 6