Construct a Matrix With Given Order

CONSTRUCT A MATRIX WITH GIVEN ORDER

Question :

Construct an m × n matrix A = [a_ij], where a_ij is given by

(i) a_ij = (i - 2j)²/2 with m = 2 and n = 3

Solution :

In general, a 2 x 3 is given by A =

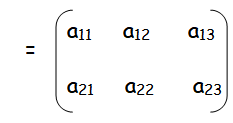
General term :

a_ij = (i - 2j)²/2

i = 1 and j = 1

a₁₁ = (1 - 2)²/2

= (-1)²/2

= 1/2

i = 1 and j = 2

a₁₂ = (1 - 4)²/2

= (-3)²/2

= 9/2

i = 1 and j = 3

a₁₃ = (1 - 6)²/2

= (-5)²/2

= 25/2

i = 2 and j = 1

a₂₁ = (2 - 2)²/2

= 0/2

= 0

i = 2 and j = 2

a₂₁ = (2 - 4)²/2

= 4/2

= 2

i = 2 and j = 3

a₂₁ = (2 - 6)²/2

= 16/2

= 8

Hence the required matrix with order 2 x 3 is

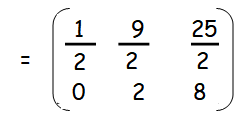
(ii) a_ij = |3i - 4j|/4 with m = 3 and n = 4

Solution :

In general, a .3 x 4 is given by A =

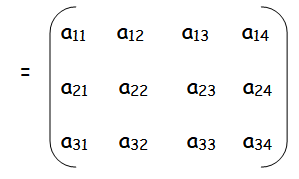
General term :

a_ij = |3i - 4j|/4

Elements of First Row

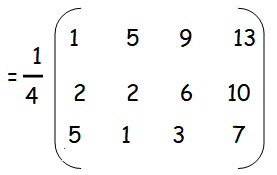
i = 1 and j = 1

a_ij = |3i - 4j|/4

a₁₁ = |3 - 4|/4

= 1/4

i = 1 and j = 2

a_ij = |3i - 4j|/4

a₁₂ = |3 - 8|/4

= 5/4

i = 1 and j = 3

a_ij = |3i - 4j|/4

a₁₂ = |3 - 12|/4

= 9/4

i = 1 and j = 4

a_ij = |3i - 4j|/4

a₁₂ = |3 - 16|/4

= 13/4

Elements of Second Row

i = 2 and j = 1

a_ij = |3i - 4j|/4

a₂₁ = |6 - 4|/4

= 2/4 = 1/2

i = 2 and j = 2

a_ij = |3i - 4j|/4

a₂₁ = |6 - 8|/4

= 2/4 = 1/2

i = 2 and j = 3

a_ij = |3i - 4j|/4

a₂₁ = |6 - 12|/4

= 6/4 = 3/2

i = 2 and j = 4

a_ij = |3i - 4j|/4

a₂₁ = |6 - 16|/4

= 10/4 = 5/2

Elements of Third Row

i = 3 and j = 1

a_ij = |3i - 4j|/4

a₃₁ = |9 - 4|/4

= 5/4

i = 3 and j = 2

a_ij = |3i - 4j|/4

a₃₂ = |9 - 8|/4

= 1/4

i = 3 and j = 3

a_ij = |3i - 4j|/4

a₃₃ = |9 - 12|/4

= 3/4

i = 3 and j = 4

a_ij = |3i - 4j|/4

a₃₄ = |9 - 16|/4

= 7/4

Hence the required matrix with order 3 x 4 is

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.