CONSTRUCT A TRIANGLE WHEN TWO SIDES AND AN INCLUDED ANGLE ARE GIVEN

Construct a Triangle When Two Sides and an Included Angle are Given :

The way of constructing a triangle is depending on the information given.

Here we are going to see, how to construct a triangle when the lengths of two sides and the angle included are given.

To construct a triangle when the lengths of two sides and the angle included are given, we must need the following mathematical instruments.

1. Ruler

2. Compass

3. Protractor

The steps for the construction of a triangle, when the lengths of two sides and the angle included are given

Construct a Triangle When Two Sides and an Included Angle are Given - Example

Construct a triangle PQR given that PQ = 4 cm, QR = 6.5 cm and ∠PQR = 60°.

Given measurements :

PQ = 4 cm

QR = 6.5 cm

∠PQR = 60°

Step 1 :

Draw the line segment QR = 6.5 cm.

(Here we take the longest side)

Step 2 :

Using protractor, at Q, draw a line QX making an angle of 60° with QR.

Step 3 :

With Q as centre, draw an arc of radius 4 cm to cut the line (QX) at P.

Step 4 :

Join PR.

Now, PQR is the required triangle.

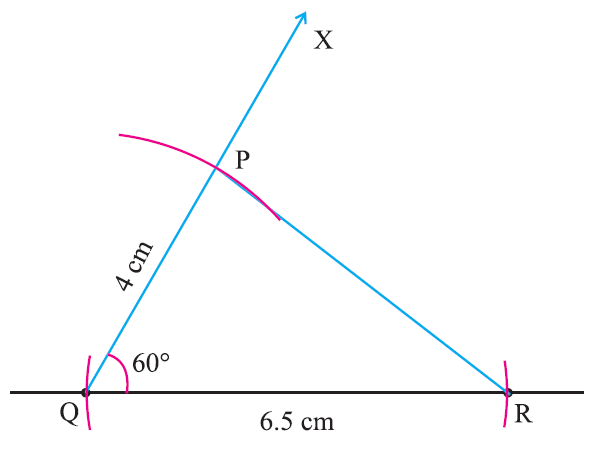
This construction clearly shows how to construct a triangle with the mathematical instruments compass, ruler and protractor when two sides and an included angle are given.

If lengths of all the three sides are given, can always we construct a triangle ?

Let us get answer for the above question with an example.

A student attempted to draw a triangle with given measurements PQ = 2 cm, QR = 6 cm, PR = 3 cm. First he drew QR = 6cm. Then he drew an arc of 2cm with Q as centre and he drew another arc of radius 3 cm with R as centre. They could not intersect each to get P.

What is the reason ?

Given measurements :

PQ = 2 cm

QR = 6 cm

PR = 3 cm

Step 1 :

Draw a line segment QR = 6cm

(Here we take the longest side)

Step 2 :

With ‘R’ as centre, draw an arc of radius 3 cm above the line QR.

Step 3 :

With ‘Q’ as center, draw an arc of c cm above the line QR

Step 4 :

Now, the arc said in step 2 and arc said in step 3 must intersect.

Let us apply the above steps and see whether the two arcs intersect.

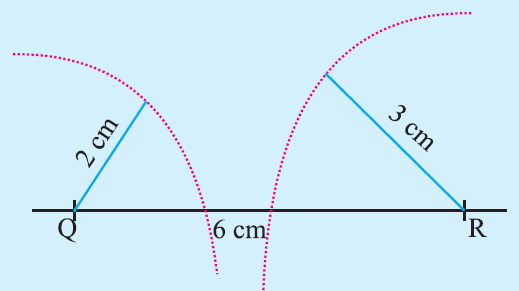
In the above figure, the two arcs said in step 2 and step 3 do not intersect.

Since the two arcs do not intersect, we can not draw a triangle with the given the three sides.

Reason :

According to the property of triangles, we have that he sum of any two sides of a triangle is always greater than the third side.

But here, the sum of the two sides 2 and 3 is less than the third side 6.

After having gone through the stuff given above, we hope that the students would have understood how to construct a triangle when two sides and an included angle are given

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

ALGEBRA

Variables and constants

Writing and evaluating expressions

Solving linear equations using elimination method

Solving linear equations using substitution method

Solving linear equations using cross multiplication method

Solving one step equations

Solving quadratic equations by factoring

Solving quadratic equations by quadratic formula