CONSTRUCTION OF ANGLE BISECTOR
In this section, you will learn how to construct angle bisector.
To construct an angle bisector, you must need the following instruments.
1. Ruler
2. Compass
Steps to Construct Angle Bisector
Step 1 :
Construct an angle of given measure at O using protractor.
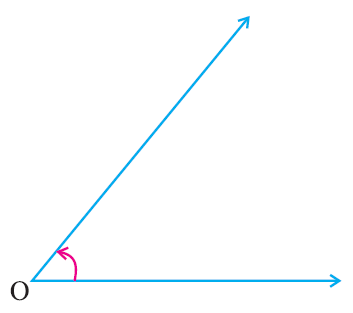
Step 2 :
With ‘O’ as center draw an arc of any radius to cut the rays of the angle at A and B.
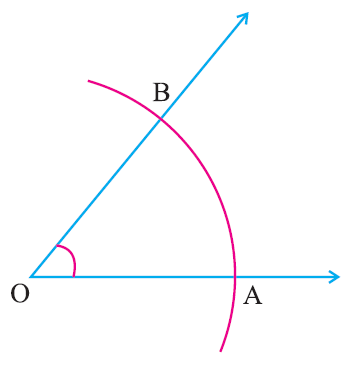
Step 3 :
With ‘A’ as center draw an arc of radius more than half of AB, in the interior of the given angle.
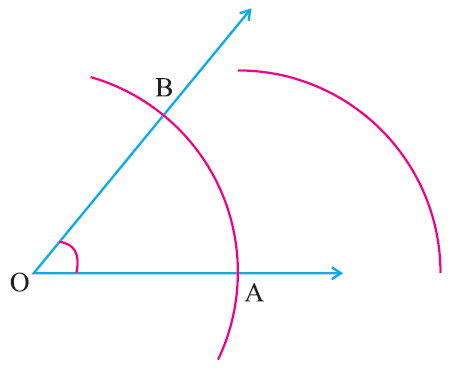
Step 4 :
With ‘B’ as center draw an arc of same radius to cut the previous arc at ‘C’.
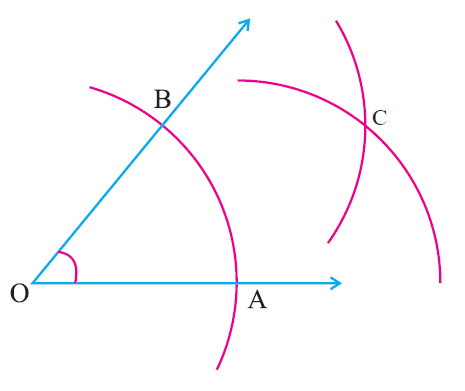
Step 5 :
Join OC.
OC is the angle bisector of the given angle.
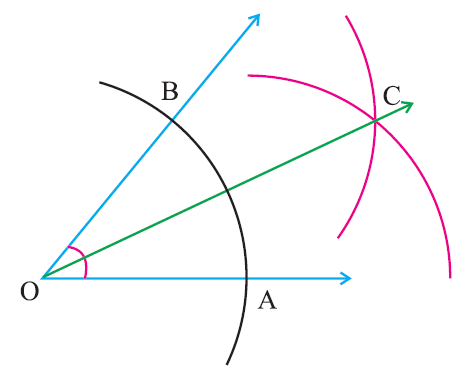
This construction clearly shows how to draw the angle bisector of a given angle with compass and straightedge or ruler. The angle bisector divides the given angle into two equal parts.
For example, if we draw angle bisector for the angle 60°, the angle bisector will divide 60° in to two equal parts and each part will measure 30°.
Key Concept - Angle Bisector
The angle bisector of a given angle is the line of symmetry which divides the angle into two equal parts.
Practice Question
Construct ∠AOB = 80° and draw its angle bisector.
Step 1 :
Construct ∠AOB = 80° angle at the point ‘O’ using protractor
Step 2 :
With ‘O’ as center draw an arc of any radius to cut the rays OA and OB at the points X and Y respectively.
Step 3 :
With ‘X’ as center draw an arc of radius more than half of XY in the interior of the angle.
Step 4 :
With ‘Y’ as center draw an arc of the same radius to cut the previous arc at C. Join OC.
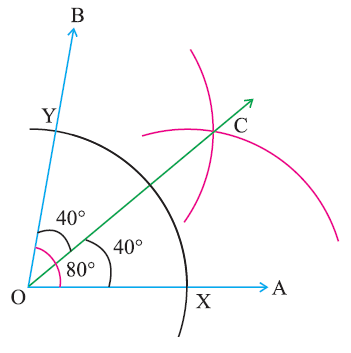
Using the steps explained above, in the above figure, angle bisector is drawn at O.
OC is the angle bisector of the given angle 80°.
Hence, OC divides the angle 80° in to two equal parts and each part measures 40°.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Integration Problems Worksheet
Mar 03, 21 07:44 AM
Integration Problems Worksheet
-
Integrating Trigonometric Functions
Mar 03, 21 06:39 AM
Integrating Trigonometric Functions
-
Practice Questions on Integration
Mar 03, 21 06:19 AM
Practice Questions on Integration
