CONVERSE OF BASIC PROPORTIONALITY THEOREM EXAMPLES

Example 1 :

In the figure given below, A, B and C are points on OP, OQ and OR respectively such that AB ∥ PQ and AC ∥ PR. Show that BC ∥ QR.

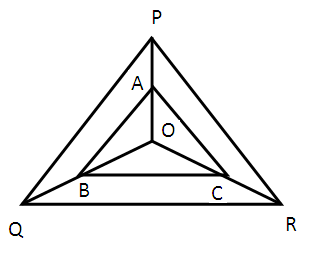
Solution :

In triangle OPQ,

Given that :

AB is parallel to PQ

OA/AP  =  OB/BQ ---(1)

In triangle OPR, 

Given that :

AC is parallel to PR

OA/AP  =  OC/CR ---(2)

(1)  =  (2)

OB/BQ   =  OC/CR

Hence the sides BC and QR are parallel.

Example 2 :

ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AO/BO  =  OC/OD.

Solution :

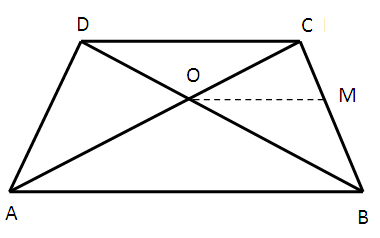
Draw OM parallel to AB meeting BC at M.

In triangle ACB,

Given that :

OM is parallel to AB

OC/OA  =  CM/MB ----(1)

In triangle BDC,

OM is parallel to CD

BM/MC  =  OB/OD

By taking reciprocals on both sides, we get 

 CM/MB  =  OD/OB ----(2)

OC/OA  =  OD/OB

OC/OD  =  OA/OB

Hence proved.

Example 3 :

The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO  =  CO/OD. Show that ABCD is a trapezium

Solution :

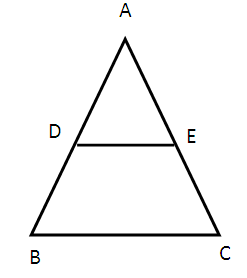
AD  =  DB

AD/BD  =  1 ---- (i)

Also, E is the mid-point of AC (Given)

AE  =  EC

AE/EC  =  1 [From equation (i)]

From equation (i) and (ii), we get

AD/BD  =  AE/EC

By using the converse of basic proportionality theorem, the sides DE and BC are parallel.

Example 4 :

ABCD is a trapezium in which AB ∥ DC and its diagonals intersect each other at the point O. Show that (AO/BO) = (CO/DO)

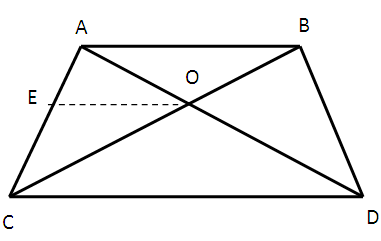
In ΔADC, we have OE || DC 

AE/ED = AO/CO  ...(i)

In ΔABD, we have OE || AB 

DE/EA = DO/BO ...(ii)

From equation (i) and (ii), we get

AO/CO  =  BO/DO

AO/BO  =  CO/DO

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.