CONVERT INEQUALITIES TO INTERVAL NOTATION

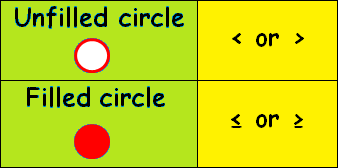
1. If we have the inequality

< (less than) or > (greater than),

we have to use the empty / unfilled circle.

2. If we have the inequality sign 

≤ (less than or equal to) or ≥ (greater than or equal to),

we have to use the filled circle.

Example 1 :

x ≤ 7

Solution :

Let us represent the given inequality in the number line.

x ≤ 7

Here, we have the sign ≤ (less than or equal). So, we have to use filled circle.

Hence the required interval notation is (-∞, 7]

Example 2 :

x ≥ -1/2

Solution :

x ≥ -1/2

Here, we have the sign ≥ (greater than or equal). So we have to use filled circle.

Hence the required interval notation is [-1/2, ∞)

Example 3 :

-8 < x ≤ 10

Solution :

-8 < x ≤ 10

Here, we are having the signs ‹ and ≤ (less than and less than or equal). So have to use unfilled and filled circle.

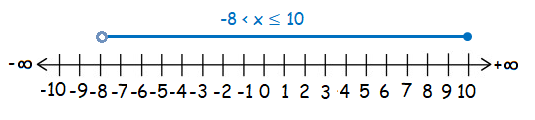
Hence the required interval notation is (-8, 10]

Example 4 :

-14 < x < -2

Solution :

-14 < x < -2

Here, we are having the both side signs ‹ (less than). So have to use unfilled circle.

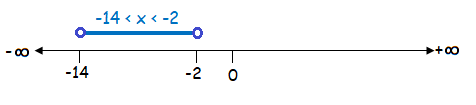
Hence the required interval notation is (-14, -2)

Example 5 :

-3/4 < x < 1/2

Solution :

-3/4 < x < 1/2

Here, we are having the both side signs ‹ (less than). So have to use unfilled circle.

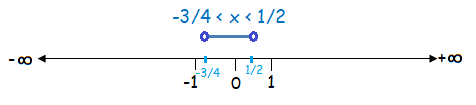
Hence the required interval notation is (-3/4, 1/2)

Example 6 :

x > 8

Solution :

x > 8

Here, we have the sign > (greater than). So we have to use unfilled circle.

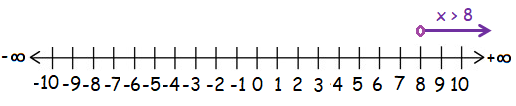
Hence the required interval notation is (8, ∞)

Example 7 :

x ≤ -2 or x ≥ 0

Solution :

x ≤ -2 or x ≥ 0

Here, both inequalities are having the sign ≤ or ≥. So we have to use filled circle.

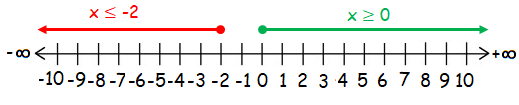
Since we have OR, we combine all the solution of both inequalities.

Hence the required interval notation is (-∞, -2] u [0, ∞)

Example 8 :

x < 0 or x > 2

Solution :

x < 0 or x > 2

Here, both inequalities are having the sign < or >. So we have to use unfilled circle.

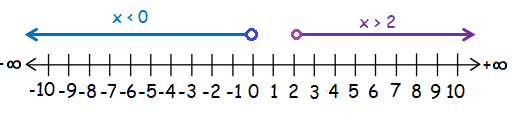
Since we have OR, we combine all the solution of both inequalities.

Hence the required interval notation is (-∞, 0) u (2, ∞)

Example 9 :

x < 27

Solution :

x < 27

Here, we have the sign < (less than). So we have to use unfilled circle.

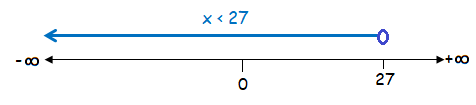
Hence the required interval notation is (-∞, 27)

Example 10 :

x > 5

Solution :

x > 5

Here, we have the sign > (greater than). So we have to use unfilled circle.

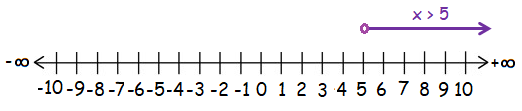
Hence the required interval notation is (5, ∞)

Example 11 :

-6 < x < 6

Solution :

-6 < x < 6

Here, we are having the both side signs ‹ (less than). So, we use unfilled circle.

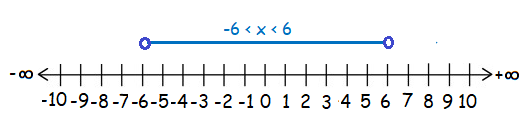
Hence the required interval notation is (-6, 6)

Example 12 :

Ryan is a wrestler trying to make weight. He currently weighs 200 lbs. If he cuts 2 lbs. per week, how many weeks will it take him to weigh less than 175 lbs.?

Solution :

Number of weeks required to weight loss = x

His current weight = 200 lbs

Weight cut by him per week = 2 lbs

The target is < 175

200 - 2x < 175

-2x < 175 - 200

-2x < - 25

x > 25/2

x > 12.5

Example 13 :

Tom is deciding whether or not he should become a member gym to use their basketball courts. The membership cost is $135.

• Members pay $2 to rent out the basketball courts.
• Non-members can rent the court also, but they have to pay $11 each time.

How many times would Tom need to rent the court in order for it be cheaper to be a member than a non member?

Solution :

Cost of membership = 135

Let x be the number of times they are using basket ball court.

Amount spent by members = 135 + 2x

Amount spent by non members = 11x

Member should be cheap than non member

135 + 2x < 11x

Solving for x, we get

135 < 11x - 2x

135 < 9x

Dividing by 9, we get

135/9 < x

15 < x

x > 15

Atleast 15 times.

Example 14 :

Daniel had $25 to spend at the fair. If the admission to the fair is $4 and the rides cost $1.50 each, what is the greatest number of rides Daniel can go on?

A. Write an inequality that represents Daniel’s situation.

B. How many rides can Daniel go on?. Justify your answer.

Solution :

Let x be the number of rides.

The maximum amount he can spent is $25.

a) 4 + 1.50x < 25

b)  Solving for x, we get

1.50x < 25 - 4

1.50x < 21

x < 21/1.50

x < 14

Daniel can go lesser than 14 rides.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.