CONVERTING COMPLEX NUMBERS TO POLAR FORM PRACTICE WORKSHEET

(1)  Write in polar form of the following complex numbers

(i) 2 + i 2√3

(ii) 3 - i √3

(iii) −2 − i2

(iv) (i - 1) / [cos (π/3) + i sin  (π/3)]       Solution

(2)  Find the rectangular form of the complex numbers

(i) [cos (π/6) + i sin (π/6)] [cos (π/12) + i sin (π/12)] 

(ii) [cos (π/6) - i sin (π/6)]/2 [cos (π/3) + i sin (π/3)]  

Solution

(3)  If (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)  =  a + ib show that 

(i)  (x₁² + y₁²) (x₂² + y₂²)............ (x_n² + y_n²)  =  a² + b²

Solution

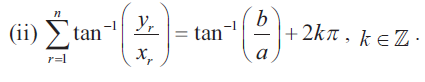
(4)  If (1 + z)/(1 - z)  =  cos 2θ + i sin 2θ, show that z = i tan θ            Solution

(5)  If cos α + cos β + cos γ = sin α + sin β + sin γ = 0, show that

(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) and

(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ) 

Solution

(6)  If z = x + iy and arg [(z - i)/(z + 2)]  =  π/4, show that x² + y² + 3x − 3y + 2 = 0.                   Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.