CONVERTING EXPONENTIAL FORM TO RADICAL FORM

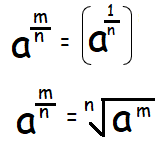
Write each expression in radical form :

Problem 1 :

m^3/5

Solution :

= m^3/5

We can write the fractional power as product of integer and fraction. So, we get

= m^{3 ⋅ (1/5)}

Power 1/5 can be used as 5^th root.

= ⁵√m³

Problem 2 :

(10x)^-3/4

Solution :

First let us write -3/4 as a product of integer and fraction.

(10x)^-3/4  =  (10x)^{-3 ⋅ (1/4)}

Changing power 1/4 as 4^th root.

=  ⁴√(10x)^-3

In order to change the negative exponent as positive exponent, we will flip the base.

=  ⁴√1/(10x)³

= 1/⁴√(10x)³

Problem 3 :

(7x)^3/2

Solution :

= (7x)^3/2

Writing the fractional power as a product of integer and fraction, we get

= (7x)^3⋅ (1/2)

Power 1/2 can be written as square root.

= √(7x)³

Here 7x is repeated 3 times inside the square root.

Accordingly the rule in square root, if we see two same terms inside the square root, we can take one out of the radical.

= √(7x) (7x) (7x)

= 7x√(7x)

Problem 4 :

(6b)^-4/3

Solution :

= (6b)^-4/3

Writing the fractional power as a product of integer and fraction, we get

= (6b)^-4⋅ (1/3)

1/3 can be written as cube root.

= ³√(6b)^-4

In order to change the negative exponent as positive exponent, we will flip the base.

= ³√1/(6b)⁴

Since it is cube root, we take one term out of the cube root for every three same terms.

= ³√1/(6b) ⋅ (6b) ⋅ (6b) ⋅ (6b)

= 1/(6b ³√6b)

Problem 5 :

8^2/3

Solution :

Method 1 :

= 8^2/3

= 8^{2 ⋅ (1/3)} 

Writing 1/3 as cube root.

= ³√8²

= ³√64

= ³√(4 ⋅ 4 ⋅ 4)

= 4

Method 2 :

When we evaluate with just numerical values in the base, we will try to write the base in exponential form.

= 8^2/3

Writing 8 in exponential form, we get 8 = 2³

= (2³)^2/3

When we have power raised to another power, we will multiply both the powers.

= 2^{3 x (2/3)}

= 2²

= 4

Problem 6 :

100^-3/2

Solution :

Method 1 :

= 100^-3/2

= 100^-3(1/2)

= √(100)^-3

= 1/√(100)³

= 1/100√100

= 1/100(10)

= 1/1000

Method 2 :

= 100^-3/2

Writing 100 in exponential form, we get

100 = 10²

= (10)^2(-3/2)

= 10^-3

= 1/10³

= 1/1000

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.