CONVERTING FRACTIONS TO DECIMALS

To convert a fraction to a decimal, check whether the denominator of the fraction is convertible to 10 or 100 using multiplication.  

If it is convertible to 10 or 100 using multiplication, you can convert the fraction to decimal as explained below. 

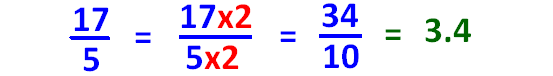
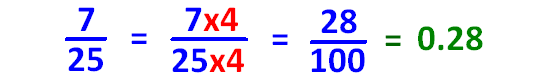
In case, the denominator is not convertible to 10 or 100 using multiplication, then we can convert the fraction into decimal using long division as shown below. 

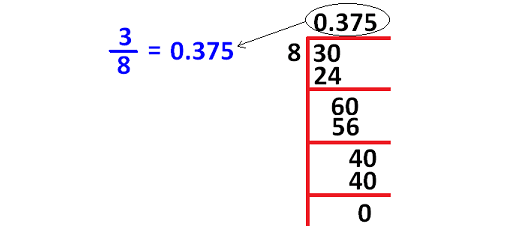
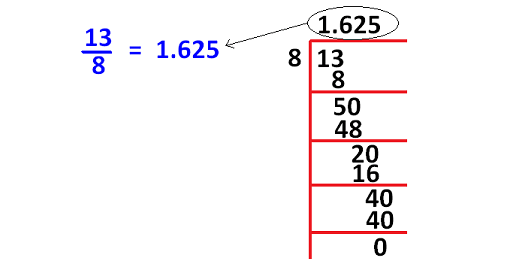
Practice Problems

overt the following fractions to decimals :

Problem 1 :

3/20

Solution : 

In the given fraction, the denominator is 20 which is convertible to 100 using multiplication by 5.

So, we have 

3/20  =  (3 ⋅ 5) / (20 ⋅ 5)

=  15/100

=  0.15

Problem 2 :

7/10

Solution : 

In the given fraction, the denominator is 10. 

So, we have 

7/10 = 0.7 

Problem 3 :

3/50

Solution : 

In the given fraction, the denominator is 50 which is convertible to 100 using multiplication by 2. 

So, we have 

3/50  =  (3 ⋅ 2) / (50 ⋅ 2)

=  6/100

=  0.06

Problem 4 :

 1/2

Solution : 

In the given fraction, the denominator is 2 which is convertible to 10 using multiplication by 5. 

So, we have 

1/2  =  (1 ⋅ 5) / (2 ⋅ 5)

=  5/10

=  0.5

Problem 5 :

 3/4

Solution : 

In the given fraction, the denominator is 4 which is convertible to 100 using multiplication by 25. 

So, we have 

3/4  =  (3 ⋅ 25) / (4 ⋅ 25)

=  75/100

=  0.75

Problem 6 :

2/3

Solution : 

In the given fraction, the denominator is 3 which is not convertible to 10 or 100 using multiplication.  

Now, we have to get the decimal form of the fraction 2/3 using long division method as explained above. 

When we do so, we get

2/3  =  0.66666..........

≈  0.67

Problem 7 :

The 1/8^th part of the money of P is equal to 1/10^th part of the money Q. If the summation of their money is 1080, what will be the difference of their money ?

a)  110    b)  120    c) 150    d) 200

Solution : 

1/8 of P = 1/10 of Q

0.125 P = 0.1Q

Q = 0.125P/0.1

Q = 1.25P

P + Q = 1080

Applying the value of Q, we get

P + 1.25P = 1080

2.25P = 1080

P = 1080/2.25

P = 480

Q = 1.25(480)

Q = 600

Difference between P and Q = 600 - 480

= 120

Problem 8 :

Convert the 0.0068 in to vulgar fraction.

a)  7/1250    b)  17/2500     c)  17/5000    d)  7/1750

Solution :

0.0068

Since we have four digits after the decimal, we have to multiply both numerator and denominator by 10000.

= 0.0068 x (10000/10000)

= 68/10000

= 34/5000

= 17/2500

So, option b is correct.

Problem 9 :

0. 023 lies between

(a) 0.2 and 0.3        (b) 0.02 and 0.03

(c) 0.03 and 0.029      (d) 0.026 and 0.024

Solution :

0. 023

0.023 lies between 0.02 and 0.03, so option b is correct.

Problem 10 :

13.572 correct to the tenths place is

(a) 10     (b) 13.57     (c) 14.5     (d) 13.6

Solution :

13.572 correct to the tenths place is

13.572

The number next to tenth place is 7 which is greater than 5. So, add one to the tenth place. Answer is 13.6. Option d is correct.

Problem 11 :

The decimal 0.238 is equal to the fraction

(a) 119/500    (b) 238/25   (c) 119/25   (d) 119/50

Solution :

= 0.238

Since we have three digits after the decimal. So, we have to multiply the numerator and denominator by 1000.

= 0.238 x 1000/1000

= 238/1000

= 119/500

So, option a is correct.

Problem 12 :

9 + 2/10 + 6/100 is equal to

Solution :

9 + 2/10 + 6/100 = 9 + 0.2 + 0.06

Adding together, we get

= 9.26

So, the answer is 9.26.

Problem 13 :

The fraction 100   27/100000 in decimal form

Solution :

= 100   27/100000

= (10000000 + 27)/100000

= 10000027/100000

Since we have 5 zeroes, we have to move the decimal 5 digits to the left.

= 100.00027

Problem 14 :

Express 11/20 as a decimal. 

Solution :

= 11/20

Since we have 20 at the denominator, we may multiply by 5 to make it as 100.

= (11/20) x (5/5)

= 55/100

= 0.55 is the decimal.

Problem 15 :

When 0.36 is written in simplest form, the sum of the numerator and denominator is ?

Solution :

0.36

Since we have two digits after the decimal, we have to multiply the numerator and denominator by 100.

= 0.36(100/100)

= 36/100

= 18/50

= 9/25

After the simplification, we get the fraction 9/25.

9 + 25 = 34

So, the answer is 34.

Problem 16 :

Megha bought 12 bags of wheat flour each weighing 4563/100 kg. What will be the total weight?

Solution :

Weight of one bag = 4563/100

= 45.63

Number of bags of wheat flour she has bought = 12

Total weight = 45.63(12)

= 547.56 kg

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.