CONVERTING POLAR TO RECTANGULAR FORM COMPLEX NUMBERS

Properties of Polar Form

Property 1 :

If z = r (cos θ + i sin θ), then

z^-1  =  (1/r) (cos θ - i sin θ)

Property 2 :

If z₁ = r₁ (cos θ₁ + i sin θ₁) and z₂ = r₂ (cos θ₂ + i sin θ₂) then

 z₁ z₂  =  r₁r₂ (cos (θ₁ + θ₂) + i sin (θ₁ + θ₂))

Property 3 :

If z₁ = r₁ (cos θ₁ + i sin θ₁) and z₂ = r₂ (cos θ₂ + i sin θ₂) then

 z_1/ z₂  =  (r_1/r₂) (cos (θ₁ - θ₂) + i sin (θ₁ - θ₂))

Find the rectangular form of the following complex numbers :

Problem 1 :

[cos (π/6) + i sin (π/6)] [cos (π/12) + i sin (π/12)] 

Solution :

=  [cos (π/6) + i sin (π/6)] [cos (π/12) + i sin (π/12)] 

=  [cos ((π/6) + (π/12)) + i sin ((π/6) + (π/12))]

=  cos (2π + π)/12 + i sin (2π + π)/12

=  cos (3π/12) + i sin (3π/12)

=  cos (π/4) + i sin (π/4)

  =  (1/√2) + i (1/√2)

=  (1/√2)(1 + i)

Problem 2 :

[cos (π/6) - i sin (π/6)]/2 [cos (π/3) + i sin (π/3)] 

Solution :

  =  [cos (π/6) - i sin (π/6)cos (π/3) + i sin (π/3)] 

  =  (1/2) [cos (-π/6)+sin (-π/6)] [cos (-π/3)+i sin (-π/3)] 

  =  (1/2) [cos (-3π/6) + sin (-3π/6)]

   =  (1/2) [cos (-π/2) + sin (-π/2)]

   =  (1/2) [0 + (-1)]

   =  (-1/2) 

Problem 3 :

If (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)  =  a + ib show that 

(x₁² + y₁²) (x₂² + y₂²)............ (x_n² + y_n²)  =  a² + b²

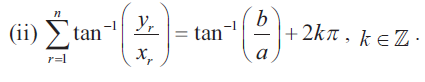
Solution :

(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)  =  a + ib

Taking modulus on both sides, we get

|(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)|  =  |a + ib|

|(x₁ + iy₁)| |(x₂ + iy₂)| |(x₃ + iy₃)|............|(x_n + iy_n)|  =  |a + ib|

√(x₁² + y₁²) √(x₂² + y₂²)√(x₃² + y₃²) ...............√(x_n² + y²)  =  √(a² + b²)

√[(x₁² + y₁²) (x₂² + y₂²)(x₃² + y₃²) ..............(x_n² + y²)]  =  √(a² + b²)

Taking squares on both sides, we get 

(x₁²+y₁²) (x₂² + y₂²)(x₃² + y₃²) ..............(x_n² + y²) =  (a²+b²)

Problem 4 :

If (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)  =  a + ib show that 

∑_{r = 1 to n} tan^-1(y_r/x_r) = tan^-1(b/a)  + 2kπ, k ∈ z

Solution :

 (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)  =  a + ib

By taking argument on both sides, we get  

arg [(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) ................(x_n + iy_n)]  =  arg(a + ib)

 arg(x₁+ iy₁) + arg(x₂+ iy₂)+................+ arg(x₂+ iy₂)  =  arg(a + ib)

tan^-1(y₁/x₁) + tan^-1(y₂/x₂) + ..................+ tan^-1(y_n/x_n)  =  tan^-1(b/a) 

∑_{r = 1 to n} tan^-1(y_r/x_r) = tan^-1(b/a)  + 2kπ, k ∈ z

Problem 5 :

Find the product

(3/2) (cos π/3 + i sin π/3) ⋅ 6 (cos 5π/6 + i sin 5π/6)

Solution :

= (3/2) (cos π/3 + i sin π/3) ⋅ 6 (cos 5π/6 + i sin 5π/6)

= (3/2) ⋅ 6 (cos π/3 + i sin π/3)  (cos 5π/6 + i sin 5π/6)

Looks like,

(cos A + i sin A)(cos B + i sin B) = cos (A + B) + i sin (A + B)

= 3 ⋅ 3 (cos (π/3 + 5π/6) +  i sin (π/3 + 5π/6)

= 9 (cos (2π + 5π)/6 +  i sin (2π + 5π)/6

= 9 (cos 7π/6 +  i sin 7π/6)

= 9 [cos (π + π/6) +  i sin (π + π/6)]

Angle lies in third quadrant, then using ASTC, we get 

= 9 [-cos (π/6) -  i sin (π/6)]

= 9 [-√3/2 -  i (1/2)]

= [-9√3/2 -  i (9/2)]

Problem 6 :

Find the product

2 (cos 9π/4 + i sin 9π/4) / 4  (cos (-3π/2) + i sin (-3π/2))

Solution :

= 2 (cos 9π/4 + i sin 9π/4) / 4  (cos(-3π/2) + i sin(-3π/2))

= (1/2) ( cos (9π/4 + 3π/2) + i sin (9π/4 + 3π/2) )

= (1/2) ( cos (9π + 6π)/4) + i sin (9π + 6π)/4) )

= (1/2) ( cos (15π/4) + i sin (15π/4) )

= (1/2) ( cos (4π - π/4) + i sin (4π - π/4) )

= (1/2) ( cos (π/4) + i sin (π/4) )

= (1/2) ( √2/2 + i√2/2 )

= (1/4) (√2 + i√2)

Problem 7 :

Find the product

(cos π/6 + i sin π/6)  (cos π/12 + i sin π/12)

Solution :

= (cos π/6 + i sin π/6)  (cos π/12 + i sin π/12)

= cos (π/6 + π/12) + i sin (π/6 + π/12)

= cos (2π+π)/12 + i sin (2π+π)/12

= cos (3π/12) + i sin (3π/12)

= cos (π/4) + i sin (π/4)

= ( √2/2 + i√2/2 )

Find the corresponding polar coordinates for the given rectangular coordinate where 0 ≤ θ ≤ 2π

Problem 8 :

(-5, -5)

Solution :

Every point will be in the form (x, y)

x = -5 and y = -5

Polar form will be in the form,

= r (cos θ + i sin θ)

r = √(-5)² + 5²

= √25 + 25

= √50

= 5√2

 θ  = tan^-1(y/x)

= tan^-1(-5/(-5))

= tan^-1(1)

= π/4

So, the required answer is

5√2 (cos π/4 + i sin π/4)

Problem 9 :

(-√3, 1)

Solution :

Every point will be in the form (x, y)

x = -√3 and y = 1

Polar form will be in the form,

= r (cos θ + i sin θ)

r = √(-√3)² + 1²

= √3+1

= √4

= 2

 θ  = tan^-1(y/x)

= tan^-1(-1/√3)

= -tan^-1(1/√3)

= -π/6

= π - π/6

= 5π/6

So, the required answer is

2 (cos 5π/6 + i sin 5π/6)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.