CONVERTING REPEATING DECIMALS TO FRACTION

Example 1 :

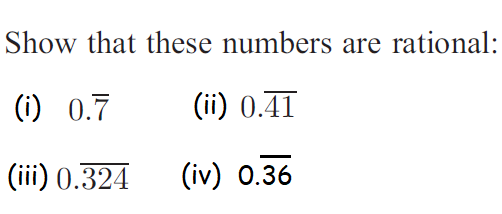
Solution :

(i)  0.77777.........

x  =  0.77777........  -----(1)

Here 7 is repeating (1 digit)

Multiply by 10 on both sides.

10x  =  7.7777......  -----(2)

(2) - (1)

10x-x  =  7.7777...... - 0.77777........

9x  =  7

x  =  7/9

So, 0.77777.....  =  7/9

(ii)  0.414141..........

Let x  =  0.414141..........    ----(1)

Here 2 digits are repeating, so we have to multiply by 100 on both sides.

100x  =  41.4141...........----(2)

(2) - (1)

100x - x  =  41.4141........... - 0.414141..........

99x  =  41

x  =  41/99

So, 0.414141..........  =  41/99.

(iii)  0.324324.........

Let x  =  0.324324.........    ---------(1)

Here 3 digits are repeating, so we have to multiply by 1000 on both sides.

1000x  =  324.324.........    ---------(2)

(2) - (1)

1000x - x  =  324.324........... - 0.324324.........

999x  =  324

x  =  324/999

So, 0.324324......... = 324/999

Example 2 :

Show 0.811111........ as fraction.

Solution :

Let x  =  0.811111........  -----(1)

Here 1 digit is repeating. So, multiply by 10 on both sides.

10x  =  8.11111........  -----(2)

(2) - (1)

10x-x  =  8.11111........ - 0.811111........ 

9x  =  7.3

x  =  7.3/9

To get rid of the decimal, we multiply both numerator and denominator by 10.

x  =  73/90

So, 0.811111........ = 73/90

Example 3 :

Show 0.5733333........ as fraction.

Solution :

Let 0.5733333........  -----(1)

Here 1 digit is repeating. So, multiply by 10 on both sides.

10x  =  5.733333........    -----(2)

(2) - (1)

10x-x  =  5.733333........ - 0.5733333........

9x  =  5.16

x  =  5.16/9

To get rid of the decimal, we multiply both numerator and denominator by 100.

x  =  516/900

By simplifying we get,

x  =  43/75

Example 4 :

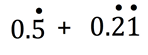
Solution :

Let x = 0.5555555........ ------(1)

Multiplying by 10 on both sides,

10x = 5.555555555..... ------(2)

(2) - (1)

10x - x = 5.555555..... - 0.555555.....

9x = 5

x = 5/9

Let y = 0.2121........... -----(1)

Multiplying by 100 on both sides

100y = 21.2121.............. -----(2)

(2) - (1)

100y - y = 21.2121........- 0.2121..........

99y = 21

y = 21/99

y = 7/33 

Adding x and y, we get

x + y = 0.5555555........ + 21.2121.............. 

= 5/9 + 7/33

= 55/99 + (21/99)

= (55 + 21)/99

= 73/99

Example 5 :

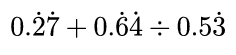
Solution :

Let x = 0.272727........ ------(1)

Multiplying by 100 on both sides,

100x = 27.2727..... ------(2)

(2) - (1)

100x - x = 27.2727.....- 0.272727........

99x = 27

x = 27/99

Let y = 0.6464........... -----(1)

Multiplying by 100 on both sides

100y = 64.6464.............. -----(2)

(2) - (1)

100y - y = 64.6464.............. - 0.6464...........

99y = 64

y = 64/99

Let z = 0.533333........... -----(1)

Multiplying by 10 on both sides

10z = 5.3333333.............. -----(2)

(2) - (1)

10z - z = 5.3333333.............. - 0.533333...........

9z = 4.8

z = 4.8/9

Multiplying the numerator and denominator by 10, we get

= 48/90

= 24/45

= 8/15

Adding x and y/z, we get

x + y/z = 27/99 + (64/99) / (8/15)

= 27/99 + (64/99) x (15/8)

= 27/99 + 120/99

= (27 + 120)/99

= 147/99

= 49/33

Example 6 :

Arrange from least to greatest :

61/330, 0.17878.........., 3^-2, 19/110

Solution :

61/330, 0.17878.........., 3^-2, 19/110

To compare these numbers, we have to convert them in same form. Let us write it as fractions.

61/330 is already in the form of fraction, so no need to change.

Let x = 0.17878........ ----(1)

Multiplying by 100 on both sides

100x = 17.878............... ----(2)

(2) - (1)

100x - x = 17.878............... -  0.17878........

99x = 17

0.17878........ = x = 17/99

3^-2 = 1/3²

= 1/9

19/110, it is already the fraction. So, no need to change.

61/330, 17/99, 1/9 and 19/110

Comparing the denominators 330, 99, 9 and 110 is 990

61/330 = (61/330) x (3/3)

= 183/990

17/99 = (17/99) x (10/10)

= 170/990

1/9 = (1/9) x (110/110)

= 110/990

19/110 = (19/110) x (9/9)

= 171/990

Comparing these fractions, 

110/990, 170/990, 171/990, 183/990

Correspond fractions are 

1/9, 17/99, 19/110, 61/330

Example 7 :

0.25151...........

Solution :

Let x = 0.25151............ ------(1)

Multiplying by 100 on both sides,

100x = 25.151.......... ------(2)

(2) - (1)

100x - x = 25.151.......... - 0.25151............

99x = 24.9

x = 24.9/99

Multiplying the numerator and denominator by 10, we get

= 249/990

After the simplification, we get

= 83/330

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.