CONVERTING REPEATING DECIMALS TO FRACTIONS WORKSHEET

Problem 1 :

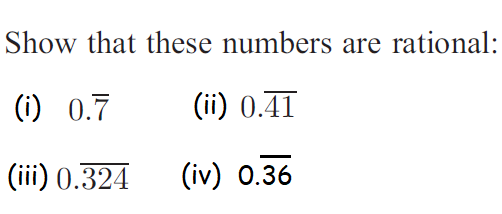
Problem 2 :

Show 0.811111........ as fraction.

Problem 3 :

Show 0.5733333........ as fraction.

Convert the following recurring decimals to fractions. Give each answer in its simplest form.

Problem 4 :

0.53333…

Problem 5 :

0.26666.........

Problem 6 :

0.08888.............

Problem 7 :

0.1353535............

Problem 8 :

0.4505050.............

Problem 9 :

0.9121212............

Problem 10 :

0.354141.........

Detailed Solution

Problem 1 :

(i)  0.77777.........

x  =  0.77777........  -----(1)

Here 7 is repeating (1 digit)

Multiply by 10 on both sides.

10x  =  7.7777......  -----(2)

(2) - (1)

10x-x  =  7.7777...... - 0.77777........

9x  =  7

x  =  7/9

So, 0.77777.....  =  7/9

(ii)  0.414141..........

Let x  =  0.414141..........    ----(1)

Here 2 digits are repeating, so we have to multiply by 100 on both sides.

100x  =  41.4141...........----(2)

(2) - (1)

100x - x  =  41.4141........... - 0.414141..........

99x  =  41

x  =  41/99

So, 0.414141..........  =  41/99.

(iii)  0.324324.........

Let x  =  0.324324.........    ---------(1)

Here 3 digits are repeating, so we have to multiply by 1000 on both sides.

1000x  =  324.324.........    ---------(2)

(2) - (1)

1000x - x  =  324.324........... - 0.324324.........

999x  =  324

x  =  324/999

Problem 2 :

Let x  =  0.811111........  -----(1)

Here 1 digit is repeating. So, multiply by 10 on both sides.

10x  =  8.11111........  -----(2)

(2) - (1)

10x-x  =  8.11111........ - 0.811111........ 

9x  =  7.3

x  =  7.3/9

To get rid of the decimal, we multiply both numerator and denominator by 10.

x  =  73/90

Problem 3 :

Let 0.5733333........  -----(1)

Here 1 digit is repeating. So, multiply by 10 on both sides.

10x  =  5.733333........    -----(2)

(2) - (1)

10x-x  =  5.733333........ - 0.5733333........

9x  =  5.16

x  =  5.16/9

To get rid of the decimal, we multiply both numerator and denominator by 100.

x  =  516/900

By simplifying we get,

x  =  43/75

Problem 4 :

0.53333…

Solution :

Let x = 0.53333......... -------(1)

Since one digit is repeating, we have to multiply by 10 on both sides.

10x = 5.3333...........(2)

(2) - (1)

10x - x = 5.3333...........- 0.53333.........

9x = 4.8

Dividing by 9 on both sides

x = 4.8/9

Since we have fraction as part of decimal, we will multiply both numerator and denominator by 10

= 48/90

Doing simplification, we get

= 8/15

So, the fractional form of the repeating decimal 0.53333........ is 8/15.

Problem 5 :

0.26666.........

Solution :

Let x = 0.2666.............-------(1)

Since one digit is repeating, we have to multiply by 10 on both sides.

10x = 2.666.............(2)

(2) - (1)

10x - x = 2.666.........- 0.2666......

9x = 2.4

Dividing by 9 on both sides

x = 2.4/9

Since we have fraction as part of decimal, we will multiply both numerator and denominator by 10

= 24/90

Doing simplification, we get

= 8/30

= 4/15

So, the fractional form of the repeating decimal  2.666............. is 4/15.

Problem 6 :

0.08888.............

Solution :

Let x = 0.08888.............------(1)

Since one digit is repeating, we have to multiply by 10 on both sides.

10x = 0.8888............(2)

(2) - (1)

10x - x = 8.8888.......- 0.8888........

9x = 8

Dividing by 9 on both sides

x = 8/9

It cannot be simplified further, then the fractional form of the repeating decimal 0.08888............. is 8/9

Problem 7 :

0.1353535............

Solution :

Let x = 0.1353535............------(1)

Since two digits are repeating, we have to multiply by 100 on both sides.

100x = 13.53535............ (2)

(2) - (1)

100x - x = 13.53535............ - 0.1353535...........

99x = 13.4

Dividing by 99 on both sides

= 13.4/99

= 134/990

= 67/495

It cannot be simplified further, then the fractional form of the repeating decimal  0.1353535........... is 67/495.

Problem 8 :

0.4505050.............

Solution :

Let x = 0.4505050.............------(1)

Since two digits are repeating, we have to multiply by 100 on both sides.

100x = 45.05050........... (2)

(2) - (1)

100x - x = 45.05050........... - 0.4505050.............

99x = 44.6

Dividing by 9 on both sides

x = 44.6/99

Multiplying both numerator and denominator by 10, we get

x = 446/990

x = 223/495

It cannot be simplified further, then the fractional form of the repeating decimal 0.4505050.............. is 223/495.

Problem 9 :

0.9121212............

Solution :

Let x = 0.9121212...... -----(1)

Since two digits are repeating, we have to multiply by 100 on both sides.

100x = 91.21212............. (2)

(2) - (1)

100x - x = 91.21212............. - 0.9121212..........

99x = 90.3

Dividing by 99 on both sides

x = 90.3/99

Multiplying the numerator and denominator by 10, we get

x = 903/990

= 301/330

It cannot be simplified further, then the fractional form of the repeating decimal 0.9121212....... is 301/330.

Problem 10 :

0.354141.........

Solution :

Let x = 0.354141.........-------(1)

Since two digits are repeating, we have to multiply by 100 on both sides.

100x = 35.4141..........(2)

(2) - (1)

100x - x = 35.4141.........- 0.354141.........

99x = 35.06

Dividing by 99 on both sides

x = 35.06/99

Since we have fraction as part of decimal, we will multiply both numerator and denominator by 100

= 3506/9900

Doing simplification, we get

= 1753/4950

So, the fractional form of the repeating decimal  0.354141.........is 1753/4950

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.