COORDINATE GEOMETRY QUESTIONS FOR GRADE 10

Question 1 :

The owner of a milk store finds that, he can sell 980 litres of milk each week at ₹14/litre and 1220 litres of milk each week at ₹16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at ₹17/litre?

Solution :

The relationship between selling price and demand is linear.

Assuming selling price per litre along the x-axis and demand along the y-axis,

we have two points, ( 14, 980 ) and ( 16, 1220 ) in the XY plane that satisfy the linear relationship between selling price and demand.

Hence, the linear relationship between selling price per litre and demand is the equation of the line passing through the points ( 14, 980 ) and (16, 1220 ) 

(y - y₁)/(y₂ - y₁)  =  (x - x₁)/(x₂ - x₁)

(y - 980)/(1220 - 980)  =  (x - 14)/(16 - 14)

(y - 980)/240  =  (x - 14)/2

2(y - 980)  =  240(x - 14)

2y - 1960 = 240x - 3360

240x - 2y - 3360 + 1960  =  0

240x - 2y - 1400  =  0

120x - y - 700  =  0

No of liters, he sells  =  17

if x = 17, then y = ?

120(17) - y  =  700

-y  =  700 - 2040

-y  =  -1340

y  =  1340

Thus, the owner of the milk store could sell 1340 litres of milk weekly at Rs 17/litre.

Question 2 :

Find the image of the point (3,8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror

Solution :

equation of line AB is, x+3y=7-----------(1)

so, the slope of line AB (m1) = -1/3 

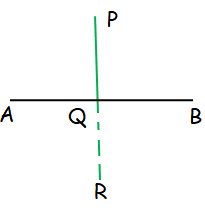
Let P(3,8) be the given point for which image to be found.

Here, PQ ⊥ AB

so, slope of PQ × slope of AB = -1 

Let slope of PQ = m 

m × (-1/3) = -1 

m = 3 

Now, equation of line PQ by using formula 

y - y₁ = m(x - x₁) 

Where, (x₁, y₁) = P (3, 8). and m = 3

y-8 = 3(x - 3)

y - 8 = 3x - 9

y - 3x + 1 = 0 --------------(2)

To determine point Q , solve equations (1) and (2).

3(1) + (2)

3x + 9y -21 + y - 3x +1 = 0

10y -20 = 0

y = 2

By applying the value of y in (1), we get

2 - 3x + 1  =  0 

3 - 3x  =  0

x  =  1

so, co-ordinate of point Q = (1,2) 

now, mid-point of P(3,8) and R (h,k) is 

  =  (x₁ + x₂)/2 , (y₁ + y₂)/2

  (3+h)/2, (8+k)/2  =  (1, 2)

comparing the co-ordinates, we get 

hence, image of point P is R (-1,-4) 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.